水文学原理第2版：经验单位线技巧

经验单位线又称时段单位线，或简称单位线（Unit Hydrograph，UH）。1932年Sherman提出了单位线的定义，即单位时段内在流域上均匀分布的单位净雨在流域出口断面所形成的地表径流过程线。在我国通常取净雨深10mm为一个单位。经验单位线本质上是线性水文系统的单位响应函数。经验单位线借助倍比和叠加假定，由已知的输入和输出来确定系统的运行特性，而不顾及净雨转化洪水过程中各个环节的物理联系。

在分析和应用单位线时，倍比和叠加假定具体叙述如下：

（1）倍比假定。同一流域上，若两次净雨历时相同，但净雨深不同，各为I1、I2，则二者所形成的地表径流过程线形状相似；即总历时相同、起涨和退水历时完全相同，相应时段的流量坐标与净雨量成正比，Qa1/Qb1=I1/I2，如图10.9（a）所示。

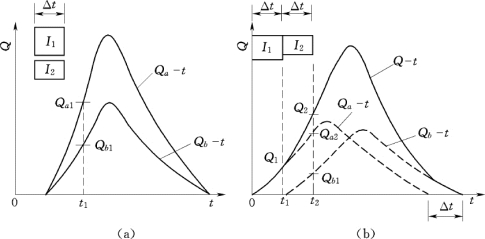
图10.9　单位线基本假定示意图

（a）倍比假定；（b）叠加假定

（2）叠加假定。同一流域上，两相邻单位时段Δt的净雨深I1、I2各自在流域出口断面形成的地表径流过程线Qa-t、Qb-t彼此互不干扰，两过程线的相应点（起涨、峰值和终止）恰好相差一个Δt，而总地表径流过程线由Qa-t、Qb-t叠加而成，例如，Q1=Qa1+Qb0，Q2=Qa2+Qb1等；如图10.9（b）所示。

依据上述假定，式（10.20）的积分简化表达为下述叠加形式：

式中：Qi为流域出口断面各时刻流量，m3／s；hj为各时段净雨量，mm；qi-j+1为单位线各时刻纵坐标，m3／s；m为降雨时段数；单位线时段数应为，i-j+1=1，2，…，n。

由两个时段净雨所形成的相应实测径流过程资料，可参照例10.1方法推求单位线。应当注意，这种反推结果受输入和输出量测误差的影响。

【例10.1】　某流域面积820km2，已知某年8月9—11日净雨和实测地表流量过程，计算时段Δt=6h，试用分析法推求单位线。

解：计算过程如表10.1所示。具体步骤如下：(www.xing528.com)

（1）将已知流量资料列入表10.1的第2栏；两时段净雨分别为I1=46mm、I2=7mm。

（2）根据基本假定，借助式（10.26）分解地表径流过程（表10.2）；将46mm和7mm净雨所形成的流量过程分别列入第3、4栏。计算过程见表10.2的注释。

（3）用10／46乘以第3栏各流量值得出检验单位线的相应流量，列于第5栏。

（4）检验由单位线求得的径流深是否等于10mm，若不符则应适当修正。本例不等，故做修正，修正后的地表径流深为

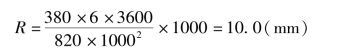
由上述计算可知，分解过程实质上是反复应用倍比和叠加假定的过程，所得出的时段单位线是一个特定的流量过程线，并非确定的数学表达式。应注意的是，当净雨时段大于3时，这种分解需要采用试错法反复计算，工作量很大。同时，由于没有确定数学表达式，也使单位线方法不便于推广。

表10.1　某流域经验单位线推求计算表

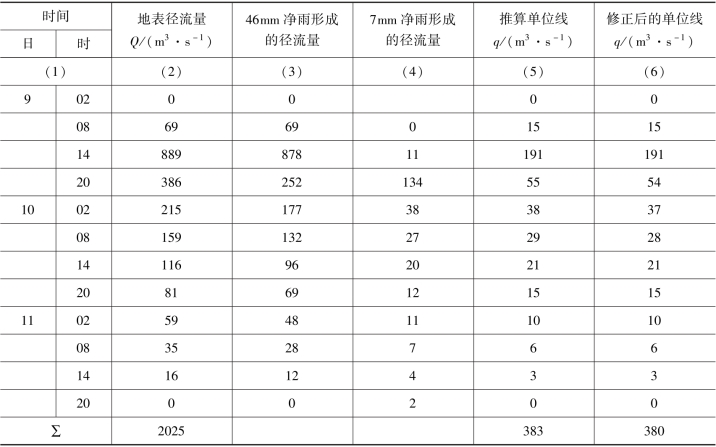
表10.2　分解地表径流过程计算表

注　*1以9日14时为例，依据叠加假定889=Qa2+Qb1；
*2再进入7mm栏依据倍比假定求得Qb1=（7/46）Qa1=（7/46）×69=11，返回46mm栏，求得Qa2=69-Qb1=889-11=878。依此类推，可求出各自相应的流量过程。

由单位线计算过程可知，所得结果是一条特定的流量过程线，并非数学方程；而且用不同净雨和流量过程所推出的单位线也不同。尽管如此，单位线由Sherman提出至今已逾七十年历史[2]，实际水文分析中仍在应用，但采用了必要的修正以考虑汇流的非线性。