水文学原理与流域汇流系统简介

通过某种关系将输入与输出联系起来的结构装置或者过程都可以称为系统，其基本概念如图10.8（a）所示。系统的形式多种多样，既可以是具体的仪器装置、电路结构，也可以是物理、化学乃至生物过程；系统的输入与输出方式也多种多样，既可以是物质，也可以是能量、信息；系统的作用在于将输入转化为输出，或者说输出是系统对于输入的响应。系统有静态与动态之分，因而研究系统必须具备参照时间。研究和应用系统的目的在于预测输出。

参照上述系统概念，可将流域汇流过程视为一种系统，其输入是净雨过程，输出是流域出口断面的洪水过程线；系统的功能则是流域的调蓄作用，如图10.8（b）所示。流域出口断面的洪水过程Q（t）即为流域系统对净雨过程I（t）的响应，简称流域响应，并可表示为

式中：Φ为运算符，表示输入与系统响应之间的特定关系。

依据流域汇流过程的物理特性推断，这一系统是一种具有因果关系的、守恒的和高阻尼的物理系统。

流域的调蓄作用，可用式（10.14）表达，将其带入流域蓄泄关系式（10.8），有

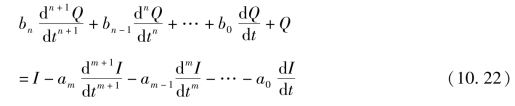
图10.8　系统与流域汇流系统示意图

（a）系统；（b）流域汇流系统

将微分算子D=d／dt引入上式，则有

式（10.23）为流域汇流系统的一般表达式[1]。(www.xing528.com)

依据系统特性，流域汇流系统又可以分为以下几种类型：

1.线性与非线性流域汇流系统

当流域汇流系统满足叠加和倍比假定时，为线性系统，否则为非线性系统。所谓叠加假定指n个输入之和所产生的总系统响应等于每个输入所产生的响应的代数和，这意味着各输入所产生的响应之间互不干扰，用数学式表达为

而倍比假定指若某一输入的n倍加之于系统，产生的响应等于原输入产生响应的n倍，即

若式（10.23）的系数am、am-1、…、a0及bn、bn-1、…、b0之中只要有一个是I和Q的函数，此方程所表达的就是非线性流域汇流系统；若所有系数都是常数，即为线性流域汇流系统。

2.时变与时不变流域汇流系统

若式（10.23）的系数am、am-1、…、a0及bn、bn-1、…、b0中，至少有一个系数是时间t的函数时，为时变流域汇流系统；当上述所有系数均为常数时，则为时不变流域汇流系统。

3.集总和分布式流域汇流系统

当把流域作为一个整体采用同一组系数进行汇流计算时，称之为集总流域汇流系统；把流域按照一定要求划分为单元（块），各单元采用不同输入或不同系数进行汇流计算，然后再按照一定方式汇总为流域出口断面流量过程时，称为分布式流域汇流系统，或称为分散式流域汇流系统。

实际流域汇流计算中常常采用几种类型的组合以反映流域汇流系统的基本特性。例如，集总时变非线性流域汇流系统，分布式时不变线性流域汇流系统，等等。

研究流域汇流系统的主要目的在于由净雨输入推求或预测流域的洪水出流过程。目前，求解流域汇流系统有3种途径，即黑箱子分析方法、概念性模型和数学物理方法。黑箱子分析方法特点在于忽略问题的物理过程，仅仅依据已有的输入和输出资料，了解系统作业的特性；例如，下面要讨论的经验单位线。概念性模型应用简化的物理概念单元，如渠道、水库等，组合构成描述系统的模型，例如随后将要讨论的Dooge模型。一般认为，数学物理方法最有前途，因为这种方法从物理途径出发建立微分方程，应用数学方法求其特定条件下的解，物理意义明确，数学解法严格，例如应用Saint-Venant方程组求解明渠非恒定流问题以及目前尚在研究中的分布式物理水文流域模型。