流域汇流面积-时间曲线：水文学原理（第2版）

假定流域中任一地点雨水的流速都相同，则任一地点净雨水质点流达出口断面的时间就取决于它与出口断面的距离。依据这一假定，将流域内汇流时间相等的点连接起来，称为等流时线，如图10.6（a）所示。它表明在同一等流时线上的净雨质点将同时流达出口断面。进一步假定，处于两条相邻等流时线之间的所有净雨质点将在这两条等流时线的时距Δτ内流达流域出口断面，而称相邻两条等流时线之间的面积为等流时面积。

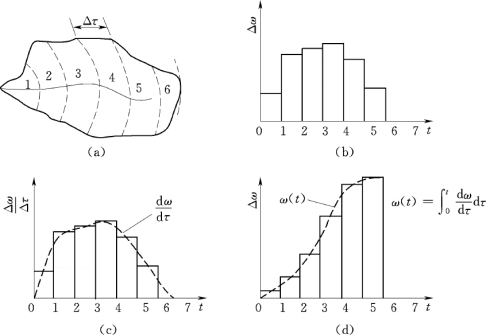
图10.6　等流时线与面积-时间曲线示意图

（a）等流时线；（b）等流时面积分配曲线；（c）面积-时间曲线；（d）累积面积-时间曲线

以等流时面积Δω为纵坐标，以流达出口断面时间为横坐标，根据等流时线图就可以绘出等流时面积分配曲线，如图10.6（b）所示。当把纵坐标选为Δω／Δτ时，即可绘出面积-时间曲线，如图10.6（c）的柱状线所示。当等流时线时距Δτ趋于无穷小时，流域汇流的面积-时间曲线就成为一条连续曲线，如图10.6（c）中的虚线所示。如果以累积等流时面积为纵坐标，可得到累积面积-时间曲线，如图10.6（d）中的柱状线所示。当Δτ趋于无穷小时，累积面积-时间曲线也是一条连续曲线，如图10.6（d）中虚线所示，此曲线方程为

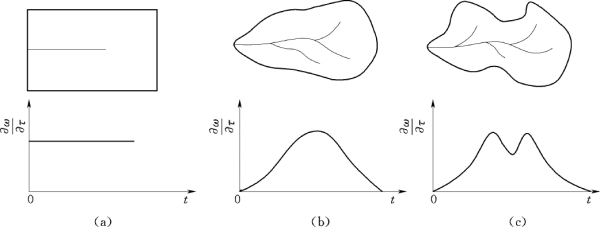
在假定流域内流速分布均一的前提下，面积-时间曲线形态就取决于流域形状。例如，矩形流域的面积-时间曲线为一水平直线，羽形流域的面积-时间曲线为一单峰曲线，葫芦形流域因两端大中间小其面积-时间曲线呈双峰状，分别如图10.7（a）、（b）、（c）所示。

(www.xing528.com)

图10.7　流域形状与面积-时间曲线

（a）矩形；（b）羽形；（c）葫芦形

由面积-时间曲线的物理概念可知，τ时刻形成的净雨对t时刻出流量有贡献的等流时面积为∂ω（t-τ）/∂τ，于是t时刻的部分出流量为

积分式（10.19）得到t时刻的流量Q′（t），即

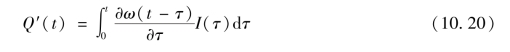
对比式（10.6）和式（10.20）可以看出，二者形式完全相同。但二者在概念上的差异在于，对于t时刻流量有贡献的净雨来自不同地点。前者认为流域内各点流速不同，τ时刻形成的净雨而t时刻流达出口断面的净雨质点散布于流域内，没有一定规律（图10.5），这些点的集合构成了形成Q（t）的汇流面积。后者由于采用了流速分布均一假定，Q′（t）是由等流时面积上的净雨形成的，而等流时面积的分布有一定规律且与流域形状有关。