一次降雨过程中,随着净雨量的增大,坡面、河网中蓄存的水量也增大。对于涨洪时段而言,净雨输入量值大于洪水流出量值。净雨停止时,坡面漫流也随之停止,这一时刻流域蓄存水量达到最大值。此后,河网汇流还将延续一段时间,在这一时段内流域蓄存水量会逐步减少。这种流域蓄存水量随着净雨过程先增加随后又减少的现象称为流域的调蓄作用。分析流域的净雨输入与出口断面的流量输出过程,可以获得直观概念,如图10.4所示。在涨洪时段内,流域蓄存水量增加。在退水时段内流域蓄存水量逐渐减少。流域这种调蓄作用是洪水过程的平移和坦化现象的原因。
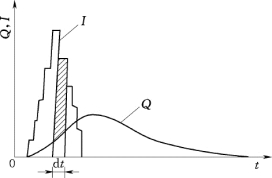
图10.4 杏子河1964年8月雨洪过程
基于上述两方面的原因,流域具有调蓄功能。一方面,雨水从各个地点降落到流域上,这些雨水质点距离出口断面远近各不相同,即使流域内不同地点的净雨质点具有相同流速,同一时刻形成的净雨也不可能同时流达出口断面。距离出口断面远的净雨质点就会暂时滞留在流域中,引起时段内流域蓄存水量的变化,导致洪水过程线的平移和坦化。另一方面,流域内各个地点的水流条件,如比降、糙率等各不相同,因此各个地点的净雨质点运动速度各不相同。所以,即使净雨质点所处位置与出口断面的距离相同,同一时刻形成的净雨也不可能同时流达出口断面。流速慢的净雨质点就会暂时滞留在流域中,引起洪水过程线的平移和坦化。
当τ时刻的净雨强度为I(τ)时,从上述分析可知,由于流域的调蓄作用,τ时刻产生的净雨不可能全部在同一时刻流达出口断面。仅流达时间为t-τ的那一部分净雨质点对t时刻的出流量有贡献,组成了t时刻出流量的一部分,如图10.5所示,因而有

由于所有0~t时段的净雨都对t时刻出流量有贡献,所以t时刻出流量Q(t)应为式(10.5)在0~t区间上的积分,即(https://www.xing528.com)
![]()
应用变量代换,上式可以写为


图10.5 等流时面积分布示意图
[图中各点的集合表示汇流面积A(t-τ)]
式(10.7)就是径流成因公式,表明不同时刻t流达出口断面的流量Q(t)不同,是由τ对应的所有汇流时间相等点上t-τ时刻的净雨所形成的。∂A(τ)/∂τ-τ在汇流理论中称作汇流曲线,它是由净雨推算流量过程的关键。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




