线性连续演算方法实证研究

1.子河段划分

实际河段往往大于特征河长，而需要将其划分为若干小段Δx，称之为子河段。一般依据该河段入流过程变化状况选定时间步长Δt，再按照Δx=CkΔt确定子河段数目。例如，河段长为L，子河段数j则为，j=L/Δx。而流量演算就是依据上边界条件（上断面的入流过程），和初始条件（t=0时刻的流量沿程分布），借助Cunge方法推求下断面流量过程。

2.入流过程处理

差分方程是微分方程的离散化方式，故需要对入流过程作时间上的离散化处理，才能进行连续演算。这就需要引入单位脉冲序列和迟滞单位脉冲序列的概念。在数学上，具有下述性质的函数称为单位脉冲序列：

式中：n仅取离散值。

具有下述性质的函数称为迟滞单位脉冲序列：

如前所述，任意入流过程均可离散化为图9.20形式。依据单位脉冲序列或迟滞单位脉冲序列，离散化的入流过程数学表达式为

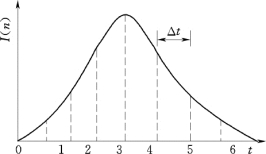
图9.20　入流过程离散化示意图

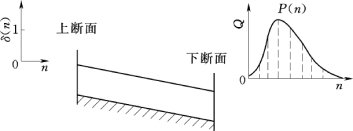
图9.21　汇流系数意义示意图

3.河道汇流系数

河段上断面入流为单位脉冲序列时，所形成的下断面出流过程一般称为汇流系数，以P（n）表示。P（n）如图9.21所示，且应满足条件：

依据线性叠加原理，某一入流过程所形成的出流过程，可用汇流系数按照下式计算

式中：Q（n）为第n个出流序列；m为入流序列个数；P（n-1）为汇流系数；j为入流序列编号，j=1，2，3，…，m。

1962年，华东水利学院就以马斯京根法分段连续演算为基础，推导出河槽汇流系数，并制成系数表供水文预报使用[5]。参照这一思路，假设每一子河段的参数C0、C1和C2相同，且初始时刻沿河各断面流量为0。故当河段上断面仅于t=0时刻有一单位脉冲入流时，可由式（9.94）求得第一子河段的下断面出流序列为

式（9.94）就是第一子河段的汇流系数。因为第一子河段出流序列，就是第二子河段的入流序列，再次应用式（9.94），可以求得第二子河段的汇流系数：

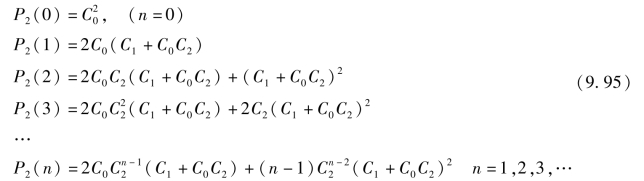
依此类推，可得出m个河段的汇流系数公式：

式中：

4.线性特征河长连续演算法

如果河段长度恰好等于一个特征河长，按照特征河长的定义，其下断面出流量与河槽蓄水量应为单值关系。若将演算河段依据特征河长分为N段，则每个单元河段与其下断面的出流量都应为单值关系，进而假定每个单元河段的这一关系均属线性，于是可将河段看作由N个线性水库串联系统（图9.22），而有

式中：Wi为各单元河段的槽蓄量，m3；Qi为出流量，m3／s；Ki为蓄泄系数。

依据水量平衡原理，可得到描述各单元河段的微分方程。(www.xing528.com)

对于第一河段

将式（9.99）代入式（9.100），有

用微分算子D表示d／dt，可解得Q1（t）

对于第二河段，其上断面入流为第一河段的出流，仿照上述方式，有

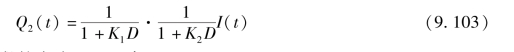
依此类推，可得到的N个河段的出流Q（t）为

若K1=K2=…=Kn=Kl，则上式成为

式中：Kl为洪水波在特征河长内的传播时间，s。

如果上断面零时刻的入流为单位瞬时脉冲时，应用拉普拉斯变换解上述高阶微分方程，即可得到线性特征河长连续演算的瞬时单位线：

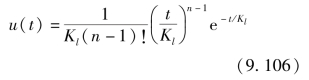
式中：e为自然对数的底。

相应的S曲线为

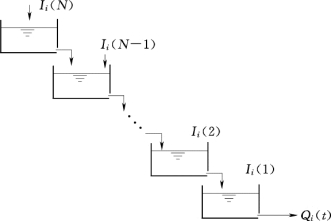
图9.22　串联水库示意图

可利用下式将其转换为时段单位线：

转换后所得的时段单位线，实际上就是特征河长连续演算的汇流曲线。若所选定的计算时段Δt很短，u（t）在Δt内变化很小，式（9.106）两端同乘以Δt，就得出特征河长连续演算的汇流系数Pm（n），即

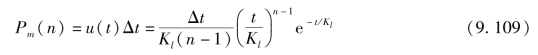
当Δt=Kl，再令m=t/Kl，上式又可转换为

此式称为标准汇流曲线，特指当计算时段取一个特征河长的汇流时间条件下的汇流曲线。

实际应用中为了简化计算，按照参数n，Kl预制S曲线表备用。然后通过式（9.108）换算为时段单位线。在此情况下，两参数n，Kl可依据物理意义参照下式计算：

式中：L为演算河段长度，m；l为特征河长，m；Ck为洪水波波速，m／s。

当河段缺乏实测水位、流量资料时，可依据河道纵断面和糙率估算，即

式中：A为过水断面面积，m2；B为水面宽度，m；s0为河底比降，‰；n为糙率系数。