入流过程的数学方程-水文学原理第2版

求解微分方程的解，需要已知初始和边界条件。其中重要边界条件就是上断面入流的洪水过程线。通常采用简单函数组合近似描述入流过程，故首先讨论入流过程的若干函数。

1.单位入流

始终保持单位强度的入流简称单位入流，一般使用单位函数或迟滞单位函数表达，后者延迟至（t-a）开始，相应定义为

两者的图形如图9.15所示。

2.单位矩形入流

在一定时段内保持单位入流强度的入流，称为单位矩形入流。矩形入流与迟滞矩形入流表达式分别为

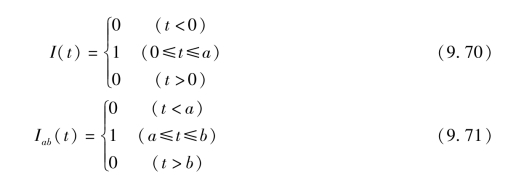
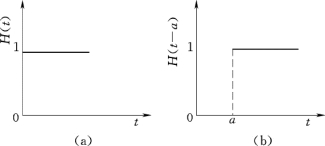
图9.15　单位函数与单位迟滞函数

（a）单位函数；（b）单位迟滞函数

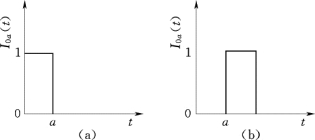
图9.16　单位矩形入流与迟滞单位矩形入流

（a）单位入流；（b）单位迟滞入流

两者的图形如图9.16所示。

3.单位脉冲入流(www.xing528.com)

当强度无穷大（I→∞），历时无穷小（t→0）而总量为一个单位时的入流称为单位瞬时脉冲入流，可用单位脉冲函数表示，即

4.单位脉冲函数与单位入流的关系

设单位时段入流函数δΔ（t）为

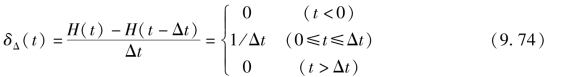
可以看出当Δt→0时，δΔ（t）就是单位脉冲函数，即

此式表明，单位脉冲函数就是入流对时间t的一阶导数。

5.入流过程近似描述

借助上述简单函数即可描述任意复杂的入流过程。例如图9.17所示流量过程，可将其分为底宽相等的若干矩形，则可用单位矩形入流表达为

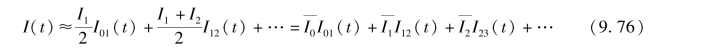
单位矩形入流与单位入流和迟滞单位入流的关系则可表达为

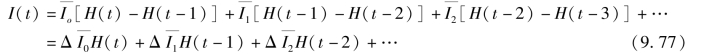
从图9.17可知，任意入流过程均可用单位矩形入流或单位入流之和逼近。显然，逼近精度取决于矩形条块的底宽，Δt越小逼近的精度越高。