特征河长原理在马斯京根河道洪水演算方法中的应用

Κалинин（加里宁）和Милюкав（米留柯夫）提出了特征河长的概念，它指在特定河长条件下，其下断面处由于水位变化引起的流量变化，与水面比降引起的流量变化抵消，从而使河段槽蓄量W与下断面流量为单值关系。提出这一概念是基于下述分析：中断面水位不变时，涨洪阶段上断面先涨，下断面后涨，下断面水位比稳定流时降低，使下断面流量减小；而此时水面比降由于有附加比降，又会使流量加大。落洪时，鉴于上断面先落，下端面后落，状况与涨洪时刚好相反；因而存在着这样一种特征河长。

由水力学可知，任意断面的流量是水位z和水面比降s的函数，即Q=f（z，s0）。取全微分，有

就特征河长而言，当中断面水位z不变时，下断面流量不变，即dQ=0，并且dz=-（1／2）lds，代入上式，故有

将式（9.58）代入式（9.57）得

而特征河长L为

式（9.60）表明，在特征河长条件下，槽蓄方程为W=K1Q，其中，K1为特征河长的传播时间，取为常数。

综上所述，特征河长是河道水力特性的综合参数。而河道水力特性也决定了洪水波运动的特点，所以特征河长与河道洪水波有着密切关系。对于宽浅矩形河道：

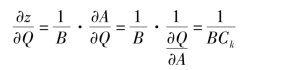
代入式（9.60），可得出

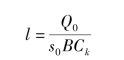(www.xing528.com)

将扩散波波速Ck与扩散系数μ表达式代入上式，得

式（9.61）表达了扩散系数μ、波速Ck与特征河长的关系。

特征河长是个重要概念，在河汇流计算中常用特征河长作为单元河段推求汇流曲线及其参数，在水文资料整编中，也利用特征河长实现水位流量关系的单值化。

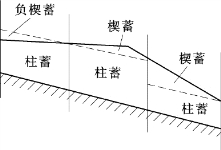
图9.14　马斯京根槽蓄量示意图

例如，马斯京根河道洪水演算方法就是基于特征河长原理，它假定，河段槽蓄量由两部分构成，一是柱蓄，即位于某平行于河底的线以下的蓄量，二是楔蓄，即此线与水面线间的蓄量；如图9.14所示。将上断面入流水量引入河段水量平衡方程，则槽蓄量可表示为入流量与出流量的函数，且槽蓄量等于柱蓄量与楔蓄量之和，于是有

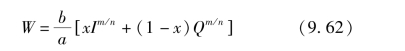
式中：a、n为河段平均水位-流量关系Q=azn中的系数和指数；b、m为河段平均水位-蓄量关系W=bzm中的系数及指数。对于宽浅矩形断面，m≈1.0；对于有漫滩的天然河道，n接近于1或小于1；x为权重系数，表示在特定槽蓄量时，入流量与出流量的相对比重，反映楔蓄对流量演算的作用，x大楔蓄作用大，x小则楔蓄作用小，若入流等于出流则x=0.5。一般天然河道的x值在0.1～0.4之间。设m/n=1.0，且b/a=k，则有

再设Q′=xI+（1-x）Q，则

式（9.63）或式（9.64）就是马斯京根法的槽蓄曲线方程，式中Q′为示储流量。

依据上述分析，可知特征河长为l时，实际河长L＞l，L=l，L＜l分别对应于河段槽蓄量与下断面流量逆时针绳套关系、单值关系和顺时针绳套关系。