河底比降与扩散波特征方程

对于河底比降s0较小的河段，附加比降∂y/∂l的作用不能忽略，两者之和比惯性项仍大时，可用扩散波描述，其能量方程可简化为

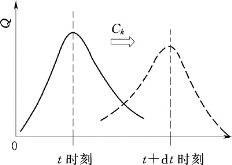
图9.6　运动波的传播与变形

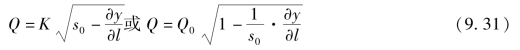
式中：Q0为稳定流时的流量，m3／s；其余符号意义同前。

若河槽为宽浅矩形，R≈y，故A=By，式（9.20）则可写为

将上式对t取导，有

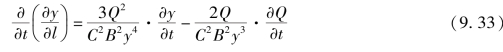
将A=By代入连续方程，得到

式（9.34）进一步对l求导数

对比式（9.33）和式（9.35），可知

(www.xing528.com)

将式（9.35）代入式（9.36），整理后有

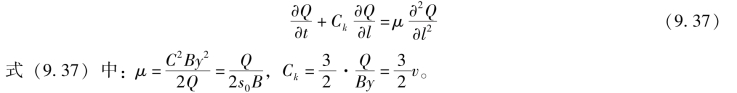
式（9.37）是关于流量Q的扩散波方程，依据微分方程特征原理，它与等价于式（9.38）和式（9.39）构成的常微分方程组

式（9.38）是扩散波特征线方程，表示扩散波以波速Ck向下游传播。式（9.39）是扩散波特征方程，因为dQ／dt≠0，故沿前进方向相应流量会产生变化，而变化程度取决于μ和∂2Q/∂l2两个因素；其中，μ为扩散系数，又称作衰减系数。当μ=0时，式（9.37）即为运动波方程，也就是说运动波属于扩散波的一个特例。

应注意，上述Ck和μ仅适用于宽浅矩形河道条件，这时扩散波的波速与运动波的相同。

将式（9.39）中的dQ／dt用差分形式表示，并注意Δt=Ls/Cp，即可导出特定河段洪峰衰减值计算式：

式中：Qp为t时刻洪峰流量，m3／s；Qp+1、Qp-1分别为洪峰前后一个时段的流量，即（t+Δt）和（t-Δt）时刻的流量，m3／s；Δt为计算时段，s。

依据上述近似，可求得长度为Ls的河段上，洪峰衰减值计算式：

它描述只有平移而不产生变形洪水波运动。当河底比降和摩阻比降接近时，或周边阻力极小，则可近似用运动波方法。