运动波方程解析解及水文学原理（第2版）

依据前述讨论，运动波方程由式（9.1）与式（9.7）联立组成，而式（9.7）也可以表达为

式中：α、m为与坡面水力特性有关的经验参数。

将式（9.8）代入式（9.1），得到

依据微分方程特征理论，它与下述常微分方程组等价：

式（9.10）是坡面运动波波速表达式，而式（9.11）表明运动波传播方向上坡面水深变化状况。该微分方程组的初始条件和边界条件应为

积分式（9.11）有

依据式（9.13）和式（9.15）可确定不透水坡

面时空分布均匀降雨所形成的坡面漫流在任意位置的

水深和流量随时间的变化状况。式（9.15）表示t=0

时刻，l=0处产生的扰动沿坡面传播的轨迹方程，即

坡面漫流运动波的极限特征线，如图9.2中实线所(www.xing528.com)

示；若t=0时刻扰动产于l=l0处，则轨迹方程变为l=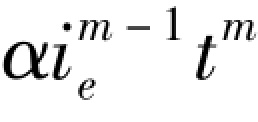+l0，其曲线如图9.2中虚线所示。

式（9.15）在l=L0则是坡面漫流运动波的最大汇流时间te，表达式为

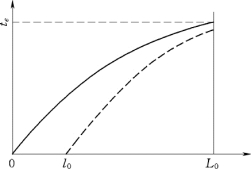
图9.2　运动波的不同特征线

于是，矩形坡面上时空均匀分布的净雨所形成的坡面出流过程为

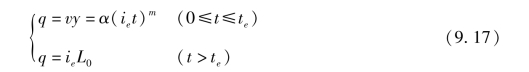
式中：q为坡面单宽流量，m3／s；t0为净雨停止时刻，此后坡面漫流处于退水阶段，则可

求解下式得到坡面出流量：

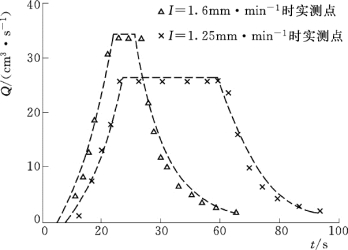
图9.3　室内不透水坡面降雨漫流实验观测与模拟过程比较

沈冰等曾用有限元法求解运动波方程来模拟室内矩形不透水坡面定雨强降雨漫流实验过程，其运动波流数k值为67，实验观测过程与运动波模拟过程拟合良好，见图9.3；并进一步模拟了黄土坡面径流实验小区的人工与天然降雨漫流过程，最小k值为115，由于天然降雨强度变化急剧引起净雨强度变化且坡面存在侵蚀现象，模拟过程与实测过程存在一定误差，但效果尚可接受，如图9.4所示[2]。由于用有限元法求解运动波方程需要详细降雨资料，特别是对于黄土坡面因下渗而使净雨强度变化很大，需要联解下渗方程和坡面漫流方程比较复杂，在尚不具备详细观测数据的水土保持工程的应用还有很多问题需要进一步研究。

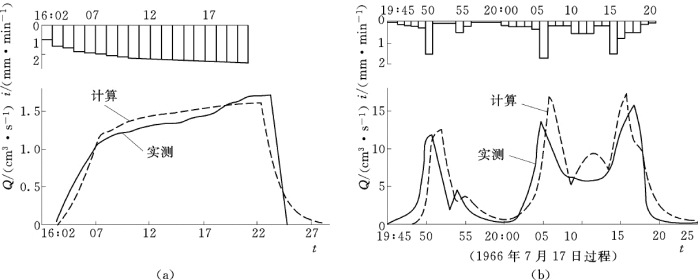
图9.4　黄土坡面变雨强漫流实验观测与模拟过程比较

（a）人工降雨-漫流实验过程；（b）天然降雨-漫流观测过程