【摘要】:依据水力学中的Saint-Venant方程组,针对降雨坡面漫流水深极浅的特点,忽略降雨造成的附加压力和沿雨强方向的流速分量,即净雨强度ie=常数,时空分布均匀降落在矩形坡面上的稳定强度净雨所形成的坡面漫流,可用连续方程和能量方程描述:图9.1矩形坡面的坡面降雨漫流式中:y为坡面水深,m;v为坡面流速,m/s;t为时间,s;l为坡长,m;ie为净雨强度,m/s;s0为地面坡度,‰;sf为坡面摩阻比降,‰;g为重力加速度,m/s2。
在相对平整,植被条件一致,坡度均匀,坡长与宽度相当的矩形坡面上,当降雨强度超过地面下渗能力或地表以下土层饱和时,会形成沿坡而下的薄层水流,通常仅几个mm,称之为坡面漫流;如图9.1所示。在水流沿坡而下的过程中,一方面雨水不断注入,另一方面也有雨水不断渗入地下或者蒸发到大气中。坡面植被或农作物使水流所受阻力较大,虽然水深很小,但坡度较大,使得水流继续向下流动。
依据水力学中的Saint-Venant方程组,针对降雨坡面漫流水深极浅的特点,忽略降雨造成的附加压力和沿雨强方向的流速分量,即净雨强度ie=常数,时空分布均匀降落在矩形坡面上的稳定强度净雨所形成的坡面漫流,可用连续方程和能量方程描述:
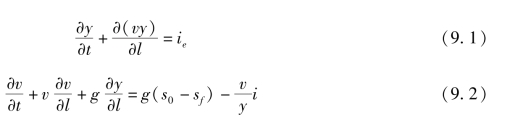
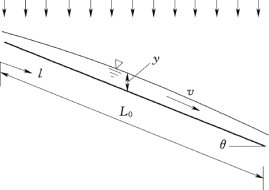
图9.1 矩形坡面的坡面降雨漫流(https://www.xing528.com)
式中:y为坡面水深,m;v为坡面流速,m/s;t为时间,s;l为坡长,m;ie为净雨强度,m/s;s0为地面坡度,‰;sf为坡面摩阻比降,‰;g为重力加速度,m/s2。
对上述两式作无因次变换,引入下述无因次变量:
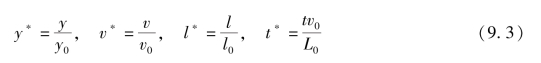
式中:y*、v*、l*、t*分别为无因次坡面水深、坡面流速、水流距离和时间;L0为坡面长度,m;y0为坡面单宽流量等于iL0时的坡面水深,m;v0为坡面单宽流量等于iL0时的坡面流速,m/s。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




