水文学原理第2版：降雨和径流关系

降雨径流关系是水文实践中推求产流量常用的一种方法。在水文水资源计算和水文预报中，为了推求一定降雨量所产生的径流量，必须建立降雨量与产流量，以及与其他影响因素之间的关系。一般常用的有降雨径流经验相关图与降雨径流模型两种途径。

8.4.3.1　饱和地面径流产流模式的降雨径流关系

图8.29　多时段降雨超渗产流过程示意图[2]

1.降雨径流相关图

根据形成一次洪水的降雨量和相应径流量所建立的降雨径流相关关系，简称为次降雨径流关系。以此类推，根据月、季、年的降雨与相应径流量建立的降雨径流关系，分别称为月、季和年的降雨径流关系。至于如何建立降雨径流相关图将在水文预报课程中介绍，下面仅介绍次降雨径流关系的有关规律和特性。

以饱和地面径流为主导机制的地区，影响产流量大小的因素为降雨量和初始土壤含水量，即

式中：R为产流量，mm；P为降雨量，mm；W0为降雨开始时刻的流域平均土壤含水量，mm。

就整个流域而言，W0很难用实测土壤含水量值来表示，在建立经验相关图时，常用反映前期流域土壤含水量大小的指标Pa来表示，Pa又称为前期影响雨量。它可根据前期的降雨和蒸发来间接推算，至于推算的具体方法也将在水文预报中作详细介绍。相关图的形式如图8.30所示。其中，图8.30（a）为以Pa为参数的形式，即R=f（P，Pa）；图8.30（b）为R=f（P+Pa）形式。

图8.30　饱和地面径流产流的降雨径流相关图

（a）R=f（P，Pa）曲线；（b）R=f（P+Pa）曲线

此类相关图应用起来比较方便，可以由P、Pa直接查算出R，进而根据降雨过程求得产流量过程。但是它仅在湿润地区和半湿润地区使用才有较好效果。因为在这些地区，地下水埋藏较浅，前期土壤缺水量不大，一次降雨很容易使包气带饱和，其产流量大小主要取决于降雨量的大小和土壤初始缺水量的大小，而与降雨强度的变化关系不大。

降雨径流经验相关图，是根据实测的雨洪资料并考虑一些主要影响因素建立的相关关系，虽然在水文分析计算和水文预报中有一定的实用价值，但是它缺乏物理基础，难以揭示产流过程中各要素的成因关系，所以在应用特别是外延时受到限制。如果以产流过程的物理概念为基础，探求产流各因素之间的数学关系，从而建立降雨径流关系的数学模型，则称为产流模型。当掌握了产流过程的理论概念以后，完全有可能从理论的角度来探求这种关系的基本形式，流域蓄水容量面积分配曲线和下渗能力面积分配曲线是建立降雨径流关系的理论基础。

2.饱和地面径流的产流模型

用特定数学方程描述流域蓄水容量面积分配曲线，如抛物线方程或指数方程，对于任一给定的降水量P和已知初始土壤含水量W0，可依据图8.27和图8.28所示的面积关系，用积分的方法求得相应的径流量R。当雨前流域平均初始蓄水量W0=0时，对于特定降雨量P，可按上述方法求得相应的R，从而可获得出一条以W0=0为参数的P-R关系曲线，如图8.31所示。若流域平均初始蓄水量W0=W1，对于特定降雨量P，可利用蓄水容量面积分配曲线，采用上述同样的方法，也可求得相应的R，从而得到一条以W1为参数的P-R关系曲线，以此类推，可建立W0=W1，W2，W3，…时的P-R关系曲线簇，如图8.31（b）所示。

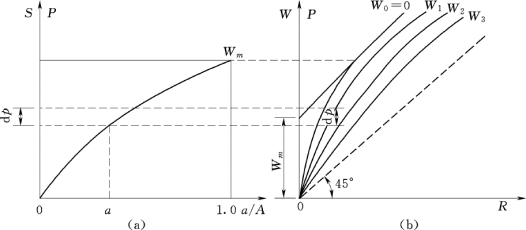
图8.31　蓄水容量面积分配曲线与降雨径流关系

（a）蓄水容量面积分配曲线；（b）降雨径流关系

由流域蓄水容量面积分配曲线的概念可知，曲线的上部为平行于P=R（即45°线）的直线，相当于全流域产流的情况，如雨前初始流域蓄水量为W0，全流域最大蓄水量为Wm，当全流域都产流时，有

这表明，当全流域产流时，其产流量与蓄水容量面积分配曲线的线型无关，仅取决于流域的缺水量（Wm-W0）。若雨前W0=0，全流域产流时的产流量为R=P-Wm，因此，对于W0=0的P-R关系曲线，其上部直线部分向下的延长线在纵轴上的截距即为Wm。关系线的下部为曲线，相当于流域部分产流的情况，在这一范围内，产流量除了与降雨量有关以外，还与蓄水容量面积分配曲线的线型有关。如降雨开始，全流域已蓄满，即W0=Wm时，R=P，它是一条通过原点的45°的直线。从图8.31中可以看出，W0=0和W0=Wm对应的两条线的上部的水平距离为Wm，因为对于W0=0时，曲线上部的方程为R=P-Wm，而W0=Wm时的方程为R=P，也就是W0=0时曲线的上部是由R=P线向左平移Wm得到的。

利用蓄水容量面积分配曲线，还可以说明一个重要的概念，即相对产流面积等于径流系数。设对应于某一W0值，产流面积为（a/F），若有降雨增量dp，其产流量为dR，由图8.31可见，dR=dp（a/F），故得

也就是饱和地面径流产流的径流系数等于其产流面积的相对值。而由P-R关系曲线可知，（dR／dP）为P-R关系曲线上某点斜率的倒数，即

式（8.43）表明，降雨径流关系曲线上任一点的斜率的倒数，等于在该点处的径流系数。由图8.31可见，曲线的下部，其切线的倾角θ＞45°，即tanθ＞1，所以径流系数α＜1，并且越向上，由于斜率越小，所以径流系数越大，而在上部直线部分，θ=45°，径流系数α=1，表示已达到全流域产流。

上面所介绍的降雨径流模型有两个待定参数：指数β和Wm，一般可通过实测降雨、径流资料率定。这些参数一旦确定，上述降雨径流关系即可确定。

8.4.3.2　超渗地面径流产流的降雨径流关系

1.降雨径流相关图

超渗地面径流的产流量，除了与当时的土壤含水量有关以外，还与降雨强度有关。所以其降雨径流相关图，需要加入反映雨强的参数，实际工作常以一次暴雨的历时或有效历时表征该次暴雨的平均雨强。图8.32为五变量合轴降雨径流相关图，其关系可表达为R=f（P，Pa，T，月份），Pa为前期影响雨量，T为暴雨历时用于表征该次降雨的平均强度。但是实践证明，对于超渗地面径流产流类型，该相关图应用效果不好。原因在于，超渗产流的产流量主要取决于降雨过程中下渗强度与降雨强度的对比，而下渗强度受到很多随机因素的影响，相关图很难全面反映这些因素，所以这种相关图往往精度较差。

2.下渗曲线法与超渗产流计算模型

超渗产流计算的基本依据是建立流域下渗能力与土壤含水量之间的关系，常称为下渗-储量关系，即

式中：fp为下渗能力，mm／h或mm／min；W为土壤含水量，mm。

建立了f-W关系，只要知道雨初土壤含水量W0，根据各时段雨量Pi，就可以推求出各时段产流量Rsi。

(www.xing528.com)

式中：fp为时段平均下渗能力，由时段土壤含水量Wi确定，mm／h或mm／min；ΔW为时段土壤含水量的增量，mm；Δt为计算时段长，h或min。

由此可见，超渗产流计算，关键在于确定fp-W关系。如果已知流域的下渗能力曲线fp-t，则可以由下式转换为fp-W关系，即

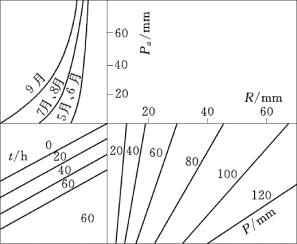
图8.32　五变量合轴降雨径流相关图

式中：Wt为t时刻的土壤含水量。

式（8.47）表明，若自供水开始时刻（t=0）起，给定不同的时刻t，计算其累积下渗量Wt，就可建立fp-W关系，其转换关系如图8.33所示。

图8.33　fp-W与fp-t间的转换关系示意图

下渗能力曲线fp-t的确定，目前常用的有水文分析法及下渗模型法两种途径。水文分析法是根据实测的降雨过程和流量过程，求得fp-W关系和fp-t关系；下渗模型法是应用下渗公式中fp-t的函数关系，再由式（8.47）转换为fp-t关系。常用的下渗公式为

依据第5章中的介绍，可将其转换为fp-W关系，则对于Horton公式：

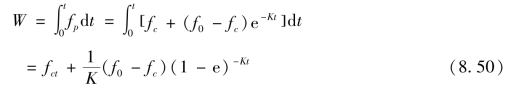
与式（8.48）联立，消去t，得

从上述式子可以看出，下渗模型有3个待定参数：最大下渗能力f0、稳定下渗率fc和系数K。这些参数可以由实测资料进行率定，然后就可以用于产流计算。

对于Philip公式，则有

与式（8.49）联立，消去t，得

式中：A、B为模型的两个待定系数。

上面所介绍的超渗产流计算模型并没有考虑产流面积在流域上的变化，因为计算时采用的是流域的下渗能力曲线。如果考虑产流面积在流域上的变化，计算还要复杂得多，在下渗公式中，还要增加反映下渗能力在流域面积上的分配与变化的参数。

从上述分析计算过程可以看出，应用下渗曲线推求各时段的超渗产流量时，需要分段进行，由于人为地划分时段有时并不能真正反映降雨强度的变化。为此提出采用下渗能力累积曲线法推求各个时段的超渗产流量。

3.下渗能力累积曲线法（时间压缩法）

下渗能力累积曲线法是利用降雨量累积曲线和下渗能力累积曲线直接推求产流量。降雨量累积曲线可以根据自记雨量资料或能反映天然降雨强度变化的时段降雨摘录资料绘制，应注意的是水文年鉴中的记录并非等时段的。这里所说的下渗能力累积曲线是下渗能力的积分表达式：

所以下渗能力累积曲线可以从已知的下渗能力曲线求得，因而也可以称为下渗量累积曲线，记为∑fp—t。

将下渗能力累积曲线与降雨量累积曲线同时使用可以较方便地求出地面产流过程及产流量。下渗能力累积曲线具有以下几个特性。

（1）任一时刻的下渗量等于土壤含水量的增加量ΔW，当初始土壤含水量W0为0时，那么下渗总量在数值上等于土壤含水量：

（2）曲线上任一点的斜率等于该时刻的下渗率，也就是任一含水量值Wt都对应一个fpt值，即

（3）任意两个含水量值之间的关系，都相应的反映了一定时距间的下渗率值的关系，即

因此，当初始土壤含水量为已知时，可以由下渗能力累积曲线确定其对应的下渗率及其相应的下渗过程；当已知含水量的变化量时，可以求出其对应的下渗的变化；若已知某一时刻的斜率，可以与同一时刻的降雨量累积曲线的斜率按产流条件判别是否产流并确定产流量。

根据上述原理，通常采用图解法来推求产流过程及产流量，可由图8.34说明。首先绘制出下渗能力累积曲线∑fp—t，根据起始土壤含水量W0值在∑fp—t线上求出A点，其时间坐标作为本次降雨的起始点绘制降雨量累积曲线，如图8.34中ABCD所示。当降雨量累积曲线的坡度大于下渗能力累积曲线的坡度时，即产生径流，反之，不产生径流，只增加土壤含水量值，相应地改变下渗率值。图8.34中AB段，因i＜fp，所以不产流，此部分雨量补充土壤含水量，将B点水平移至下渗量累积曲线上的B′点，对于BC段，i＞fp，所以产流，将BC平行移到B′C′，则过C′点的垂直线与∑fp—t曲线交于C″，那么C′C″就是BC段雨量所产生的径流深。再将CD平行移至C″D′，由于其坡度小于∑fp—t曲线的坡度，因此CD段不产流，依次逐段计算。凡平移后的时段降雨末端在∑fp—t上方者为产流降雨，其量值等于末端沿垂线至∑fp—t曲线交点的长度，如C′C″；凡平移后的时段降雨末端在∑fp—t下方者，则不产流，该时段降雨量全部为入渗量。

在上面介绍了降雨径流关系，从分析研究降雨径流关系的过程可以看出，分析研究影响流域产流的因素对于建立降雨径流关系是非常重要的。