土壤水下渗曲线经验公式-水文学原理

以上下渗曲线的确定均是基于Richards基本方程的理论推导获得，通过推导过程，有助于认识下渗的物理机制和规律。但这些推导过程均是对问题做了一定简化，因此对于实际复杂情况应用起来误差较大。在实际应用中，下面介绍一些有代表性的经验下渗曲线公式。

1.Kostiakov公式

1931年，苏联学者Kostiakov提出了如下的经验公式：

式中：fp为实际下渗率；t为下渗时间；A，b为经验常数，与土壤质地有关，可通过实验确定。

从式（5.40）可以看出，下渗过程中，随下渗时间的延长，下渗率逐渐减小，且呈幂函数曲线关系，这与实际情况一致，但当t→∞时，fp→0，则与实际情况不相符。

2.Horton公式

1940年，Horton提出了反映降雨产流过程中，下渗率与初渗率、稳渗率以及时间t之间关系的经验公式，即

式中：fc为稳定下渗率；f0为初始下渗率；β为经验参数，反映了入渗率由f0减小到fc过程中的快慢程度，其他符号意义同前。

根据式（5.41），当t→0，fp→f0，因此f0称为初渗率；当t→∞，fp→fc，故fc为稳渗率。Hortan公式的这一特点使得其具有较广的适用范围，既适用于一个点的下渗，也适用于流域范围内的下渗。(www.xing528.com)

3.Holtan公式

1961年，Holtan提出的经验公式如下：

式中：W为一定厚度的土壤在下渗开始后所能容纳的下渗水量；F为累积下渗量；d为土层厚度；α、β为经验参数；其他符号意义同前。

Holtan公式与其他公式的不同在于它只适用于流域范围内的下渗，而不适用于点的下渗。在应用时主要的困难在于控制土层的确定。

4.Smith公式

Smith根据土壤水分运动的基本方程，对不同质地的各类土壤，进行了降雨入渗模拟实验，在大量实验的基础上，于1972年提出了如下的下渗公式：式中：R为降雨强度；tp为开始积水的时间；t0为下渗的初始时间；B，β为经验参数；其他符号意义同前。

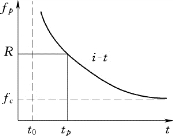
图5.10　Smith公式下渗率fp与时间t的关系

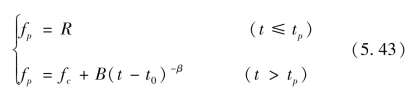
式（5.43）表示，在下渗初期，下渗主要由供水强度控制，实际下渗率即等于降雨强度R；在tp时刻以后，即地面开始产生积水或出现径流以后，下渗主要由土壤决定。下渗率随时间的变化如图5.10所示[4]。图中显示，当t→∞，fp=fc。因此，fc理论上也等于饱和水力传导度KS。当t→t0时fp→∞，故t0为下渗曲线的渐近线所对应的时间坐标。