水文学原理（第2版）：饱和土壤水下渗理论

饱和下渗理论模式是由Green和Ampt提出的。他们对下渗过程做了如下简化：首先，土壤为均质各项同性，初始含水率极低且在剖面上均匀分布；其次，入渗一开始就有积水，且不随时间而变化；此外，湿润锋面是饱和土壤与非饱和土壤的交界面，即湿润锋上部区域的土壤含水率为饱和含水率，下部区域仍为初始土壤含水率。

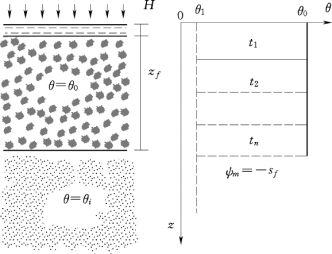
图5.9　概化的湿润锋移动

在以上假设条件下，下渗过程中土壤水分剖面随时间的变化将形如一个汽缸中的活塞不断地沿深度方向推进，如图5.9所示。若以地表为参考平面，取向下为正。在上述假设条件下，可根据水流的达西定律及水量平衡方程建立饱和下渗基本模式。现在具体分析一下地表和湿润锋处任意两点之间的水势情况。根据假设条件，地表的积水深度为H，则土表某一点单位质量水分所受的压力势为H。由于无其他水势。因此，地表处某一点的总水势仍为H。同样，湿润锋面处某一点受到下方土壤水的基质势为ψm，若以吸力来表示则为-sf；若重力势以其下渗的深度zf表示，则总水势为-sf-zf。因此，土壤表面与湿润锋面之间的水势梯度为（-sf-zf-H）/zf，此水势梯度即为下渗水流运动的动力。

根据达西定律，则下渗率可表示为

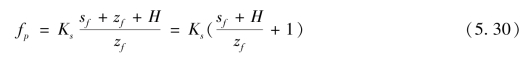
式中：fp为下渗率或下渗能力，cm／d；Ks为饱和水力传导度，cm／d。

式（5.30）表示饱和下渗过程中下渗率与湿润锋的关系。下面针对不同情况分别求下渗率及累积下渗量随时间的变化关系式。

1.积水深度较小或下渗时间较长

当积水深度较小，或下渗时间较长时，H相对于zf很小。因此，式（5.30）可近似为

此外，根据假设，土壤剖面初始含水率分布均匀。下渗过程中，水流经过的地方，土壤含水率均达到饱和含水率，根据水量平衡原理，则下渗过程中累积下渗量F应为

式中：θs为饱和体积含水率，cm3／cm3；θi为初始体积含水率，cm3／cm3。

由式（5.32）可得

将其代入式（5.31），可得

(www.xing528.com)

式（5.33）反映了下渗率和累积下渗量之间的关系，是饱和下渗理论基本模式之一，根据定义，fp=dF/dt，则式（5.33）可变为

以下渗开始时刻为0，自0→t，0→F对式（5.33）取积分，得

对其积分后得

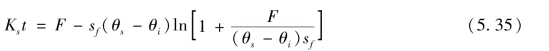
式（5.35）即为积水深度较小或下渗时间相对较长时的饱和下渗过程中累积下渗曲线的表达式。

2.下渗时间较短

当下渗的时间较短时，zf相对于sf+H来说较小，此时式（5.31）可近似为

根据下渗率与累积下渗率的关系，对式（5.32）求导，并联立式（5.36）可得

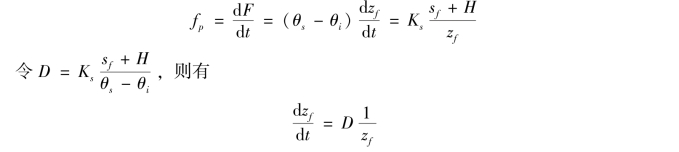
对上式积分后得

将式（5.37）分别代入式（5.32），得

对式（5.38）求导，得可以说饱和下渗过程是一种比较理想的下渗模式，与实际情况下砂性土壤的下渗过程较为相似，但与黏性土壤的下渗过程差异较大。