非饱和土壤水下渗理论(水文学原理第2版)

推导非饱和土壤水流运动的下渗方程时，若以地面为标准参考面，坐标原点设在地面，取向下为正。根据土壤水分运动的连续方程式（5.19），只考虑垂向一维水流情况下，非饱和土壤水流运动的下渗方程为

式（5.22）是一个非线性偏微分方程。对于此式，只有在一些特殊情况下才能求得其解析解。下面以忽略重力作用为例分析其下渗方程的解。

对于此式的求解，首先要结合某一具体下渗过程给出其初始和边界条件。假定此下渗过程所构成的定解问题如下：

对于此问题，可分为以下两种情况进行求解。

1.假定扩散率为常数

为了简化，可假定D（θ）为常数，即令D（θ）=D，通过Laplace变换和逆变换可求其解析解，结果为

根据式（5.25）就可以求出任一时间，任一位置z处的含水率θ（z，t）。知道了θ（z，t），就可求出其下渗曲线，现举例说明如下。

根据图5.8，在忽略重力作用时，图中阴影部分的面积即为Δt时段内土壤的累积下渗量，即

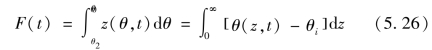(www.xing528.com)

将式（5.25）代入式（5.26），整理后得

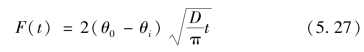
图5.8　半无限长土柱的下渗过程

对式（5.27）求导，得

式中：fp为下渗率，cm／d。

式（5.28）就是忽略重力作用、扩散率为常数时下渗曲线的表达式。

2.扩散率不为常数

当扩散率不为常数时，式（5.24）的求解过程比较复杂，必须借助计算机，因此，不再做具体介绍。但下渗曲线的求解思路与前面相同，即通过计算模拟求出任一时间和任一位置的含水率θ（z，t）分布剖面。根据θ（z，t）求出其下渗曲线，结果为

式（5.29）就是忽略重力作用、扩散率不为常数时下渗曲线的基本表达式。

对比式（5.29）与式（5.28），可以看出忽略重力作用下，无论扩散率是常数还是变数，下渗率fp均为t-1／2的函数，且当t→∞时，fp→0，而在实际下渗过程中，当t→∞时，fp→fc，因此，忽略重力只能适用于下渗时间较短的情况。