混凝土徐变系数及其防裂方法的研究成果

1.抗压强度与等效龄期成熟度的经验关系

在实际的设计中,构件主要利用的是混凝土较强的抗压性能;抗压强度最易测量,最为直观,混凝土的其他力学性能,如弹性模量和抗拉强度等常常表示成抗压强度的函数。根据相关试验研究发现,混凝土的养护温度和龄期对抗压强度的发展具有重要影响,基本规律是:抗压强度随龄期的增加而增长,早期混凝土抗压强度发展速度随养护温度的增长而加快,其规律与混凝土的水化放热特性类似。众多研究者根据试验经验建立了基于Arrhenius函数和等效龄期的混凝土抗压强度计算模型,主要有以下5种。

(1)线性模型[169]:

式中:h为与混凝土强度和水泥种类有关的系数;M意义同式(4.1)。

(2)对数模型[178]:

式中:a、b为与水灰比和水泥种类有关的常数;M意义同式(4.1)。

(3)双曲线模型[179]:

式中:(f c)max为最终抗压强度;k为常数;te为等效龄期;t 0为初凝等效龄期(零强度等效龄期)。

(4)指数式模型[180]:

式中:各参数物理意义同式(3.20)。

(5)复合指数式模型[181]:

式中:f c,28为混凝土标准养护条件下28d龄期的抗压强度;s为与水泥类型有关的系数,一般水泥取0.25,速硬水泥取0.20,缓硬水泥取0.38。

以上模型存在着各种不同的优缺点:直线方程法使用比较简便,但适用于50～30℃的范围,而水泥水化及硬化过程是随着时间逐渐减慢的,很难说它们是呈线性关系,而且养护温度与养护时间对强度的影响不能等量齐观,说它们之间是线性关系是不真实的;对数模型缺点在于,当混凝土的成熟度M趋于无穷大的时候,强度f也将无限增大,而当M=0时,f≠0,这与实际不符;复合指数式模型的缺陷是,仅以混凝土28d抗压强度来控制早期强度发展过程,适应性较差,该模型没有考虑混凝土的初凝时间。综上所述,双曲线模型[式(4.10)]和指数模型[式(4.11)]具有较多的优点,同时考虑了成熟度与混凝土的初凝时间。

2.抗压强度模型的推导和完善

抗压强度模型[式(4.10)]是由Knudsen用一种完全不同的方法,即水泥水化度的概念,从理论上推导的,详见文献[182]。在推导过程中,考虑了不同水泥颗粒各自的动力反应和水泥颗粒的粒径分布。推导的主要假设如下。

(1)所有的水泥颗粒在化学性能上都是一样的,只是其粒径大小不同。

(2)水泥颗粒独自地进行化学反应,不相互影响。

(3)水泥颗粒的粒径分布可以用一双曲函数表示。

(4)不同水泥颗粒各自的动力反应也可以用一双曲函数表示。

前面已经交代,双曲线的抗压强度模型具有很强的适用性,不足之处在于将混凝土活化能E作为一个常数考虑。本书在此模型的基础上,将混凝土活化能的变化考虑到模型中,推导并完善抗压强度模型。

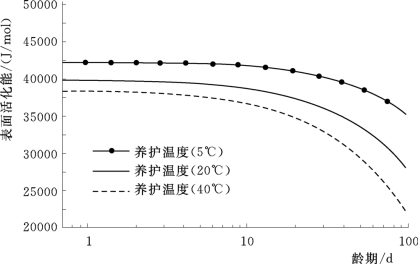
Jin Keun Kim在试验基础上(图4.2)建立了如下活化能函数[183-184]:

式中:Ea为混凝土活化能;Ea0为初始混凝土活化能;αE为待定参数。

Ea0、αE分别满足:

式中:T为混凝土温度,℃。

(www.xing528.com)

图4.2　养护温度和龄期对混凝土表面活化能的影响

根据式(4.4)和式(4.13),可得

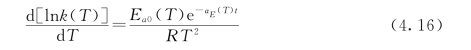
式中:k(T)为水化反应速率;T为混凝土的绝对温度。

在t龄期,当温度分别为T 1和T 2时,水化反应速率之比k 1/k 2可以表示为

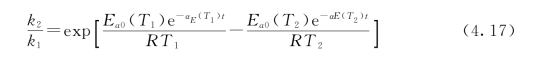
从而有

式中:te为考虑混凝土表面活化能随水化反应变化的等效龄期;t 0为混凝土初凝时间,t 0=0.66-0.011T≥0;T r为参考温度,一般取20℃;T为混凝土温度,℃。

具体计算时,可离散为式(4.19)的形式:

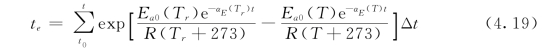
在此基础上,将式(4.19)代入式(4.10)便可得到完善的混凝土抗压强度模型。

3.成熟度影响的抗压模型应用

试验来源于文献[185],试验的混凝土设计强度等级为C40,试件养护温度为23℃,抗压强度试验的龄期为12～23h、1d、2d、3d、7d和28 d,试验结果见表4.1

表4.1　C40混凝土各龄期抗压强度

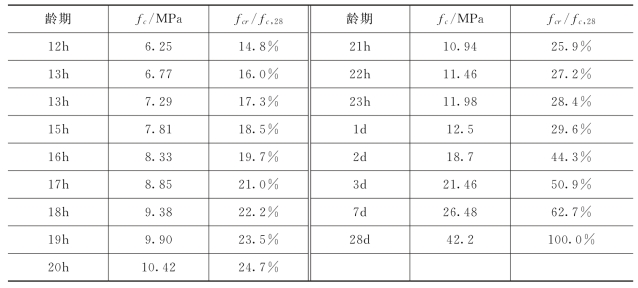
需要强调的一点是,目前国外尚未对关于温度对混凝土最终抗压强度的影响程度形成统一认识。1997年,Chanvillard提出了28d龄期抗压强度与养护温度的关系(混凝土水灰比为0.45且无火山灰掺合料)[182]:

式中:f c,28(T)为养护温度为T时混凝土28d龄期抗压强度;f c,28(20)为养护温度为20℃时混凝土28d龄期抗压强度。

式(4.20)是在恒温养护条件下得到的,从表达式来看,混凝土养护温度每升高1℃,28d龄期抗压强度比标准养护条件下降低1%,降低幅度是比较大的。在实际结构中,混凝土温度处于不断变化中,早期温度快速升高,后期温度缓慢下降,最终抗压强度受养护温度的影响可以忽略不计[188]。基于等效龄期的抗压强度公式的推导过程如下。

根据抗压强度与等效龄期的关系式(4.10),在试验过程中,取参考温度T r与养护温度相同,即T r=23℃,那么根据式(4.19),te=t,则式(4.10)改写成如下形式:

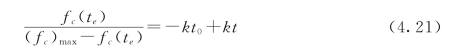
式(4.21)有3个未知参数需要确定,分别是(f c)max、k、t 0,下面一一确定这3个参数。

(1)参数(f c)max、k的确定。混凝土的最终强度(f c)max可以用较晚龄期(3d后)的试验数据进行估计,在较晚龄期,近似上(t-t 0)=t,式(4.21)可以写成:

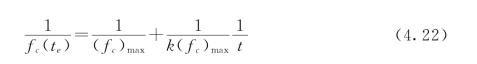
从式(4.22)可知是线性关系,直线在　轴上的截距就是(f c)max的倒数。根据表4.1中3d后的试验数据作图4.3,对数据进行线性回归,得到y=0.0734x+0.0235,那么0.0235,则(f c)max=42.55MPa。根据该拟合直线的斜率0.0734,容易知道k=0.3201。

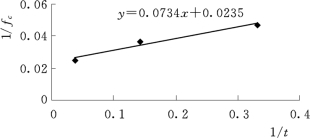
图4.3　抗压强度的倒数与龄期倒数线性回归

(2)参数t 0的确定。将(f c)max、k的值代入式(4.10),根据表4.1中的试验数据,用统计软件SPSS非线性回归参数t 0=0.04,那么得到抗压强度公式:

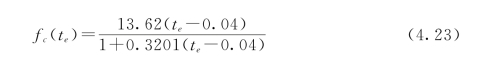
其中te的取值参照式(4.19),对于试验所用混凝土,不管温度与时间如何组合,只要在参考温度的等效龄期相等,其抗压强度也是相等的。