混凝土徐变系数的研究和在防裂方法中的应用

当某一种混凝土的组成成分和生产工艺确定后,强度的增长因素主要取决于温度和时间。早在1951年,Saul[169]总结了前人关于蒸养混凝土的研究理论与实验结果,把混凝土的养护温度与时间的乘积定义为混凝土的成熟度,提出了成熟度的概念。Saul认为,混凝土的成熟度应该从混凝土硬化的起始温度开始计算,并给出了如下的计算公式:

式中:M为混凝土在t时刻的成熟度;T为在Δt时间内混凝土养护的平均温度,℃;T 0为混凝土硬化的起始温度,℃。

式(4.1)被称为Nurse-Saul方程。式(4.1)认为,在Δt的时间间隔内,只有当混凝土的温度大于混凝土硬化的起始温度时,混凝土的力学性能才开始发展。把混凝土的温度和时间的关系用成熟度曲线表示,如图4.1所示。由式(4.1)可知,混凝土在t时刻的成熟度,在数值上等于t时刻内混凝土的温度与混凝土硬化的起始温度围成图形的面积。

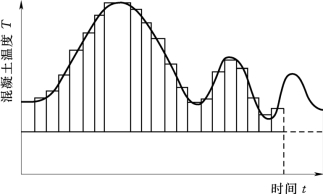
图4.1　Saul的成熟度方程示意图

1953年,S.G.Berstorm根据Saul方程,在对一系列抗压强度试验结果进行归纳分析后,建议把-10℃作为混凝土硬化的起始温度,并认为混凝土的成熟度方程可以用于常温养护条件下的混凝土。此外,Saul还提出了著名的Saul准则:一定配合比的混凝土,不管温度与时间如何组合,只要成熟度相等,其强度也是相等的。Nurse-Saul方程可以把不同的养护温度—时间历程换算成在参考温度下达到相同成熟度所需要养护的等效龄期历程,计算方法如下:

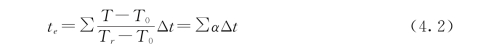
其中

式中:te为参考温度下的等效龄期;T r为参考温度,℃。

α称为龄期转换系数,例如,如果T 0为-10℃,在温度为39℃的条件下养护2h,等效于在25℃的条件下养护1.4×2h,其中,α=1.4。从α的表达式可以发现,龄期转换系数α被定义为养护温度的线性函数,但这与实验结果略有偏差。α是由Nurse-Saul方程推导出来的,也从一方面说明Saul的成熟度方程存在不足的地方。

所谓等效龄期(成熟度)就是在其他温度下,达到相同水化程度所需要的时间等效于在参考温度下所需要的时间[170]。一般情况下,温度越高,水化反应越快,达到相同的水化程度所需要的实际龄期越短,即相同的实际龄期温度越高成熟度越大,即等效龄期越大,反之亦然。对于混凝土的徐变而言,等效持荷时间就是在其他温度下,达到相同徐变应变时所需要的持荷时间等效于在参考温度下所需要的持荷时间[171]。

1954年,Rastrup[172]根据物理化学中所熟知的规律“如果温高10℃,化学反应速度将提高1倍”,提出了等效龄期计算方法:(www.xing528.com)

根据式(4.3)的计算方法,混凝土在39℃的条件下养护2h,等效于在25℃的条件下养护5.278h。然而,Wastlund[173]指出,在很大的温度范围内,不同温度—时间历程对混凝土力学性能的影响计算中,Rastrup方程的准确性不如Nurse-Saul方程。

1960年,Copeland[174]等提出,水泥和水的反应是放热反应,可以用化学反应中的Arrhenius方程来描述温度对水泥化学反应速率的影响,即

式中:k(T)为水泥与水的化学反应速率;A为前因子;T为反应温度,℃;R为气体常数,8.3144J/(mol·K);E为化学活化能,mol-1。

Freiesleben Hansen和Pedersen于1977年提出基于Arrhenius函数的等效龄期成熟度函数[175],形式如下:

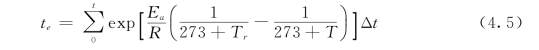
式中:T r为混凝土参考温度,℃,通常取20℃;T为Δt内的混凝土平均温度,℃;te为相对于参考温度的混凝土等效龄期成熟度,d。

后来,Freiesleben Hansen和Pedersen完善了上述模型并建立了如下积分形式的等效龄期成熟度模型:

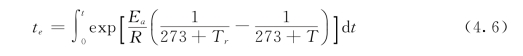
该模型即为在国外较为普遍采用的等效龄期成熟度模型,具体计算时,可离散为式(4.5)的形式。

在式(4.5)中,指数部分代表用绝对温度表示的龄期转换系数,其中化学活化能E,根据Freiesleben Hansen和Pedersen的建议,可以取值如下:

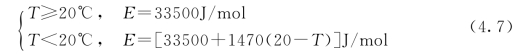
事实上,在水化反应过程中,反应活化能Ea不是常数,而是与温度有关,这种变化对混凝土的水化放热特性影响较小,可以忽略不计,但对混凝土强度等力学特性的影响较大,需要在计算模型中加以考虑,具体的考虑将在下节讲述。根据上面的计算方法,混凝土在39℃条件下养护2h,约等效于在25℃条件下养护3.65h。Byfors[176]和Naik[177]指出,在很大的温度范围内基于Arrhenius方程的等效龄期的计算方法,比Rastrup方程、Nurse-Saul方程及其他方程,能更好地反应养护温度和龄期对混凝土性能的影响。尽管水泥的水化反应过程并不是简单的化学反应过程,但是工程实践和实验表明,与其他方程一起使用,基于Arrhenius方程的等效龄期的计算方法能方便而正确地计算不同的温度和龄期作用下的混凝土力学性能。鉴于上述理由,本书采用式(4.6)计算混凝土的等效龄期。