混凝土徐变系数研究及应用

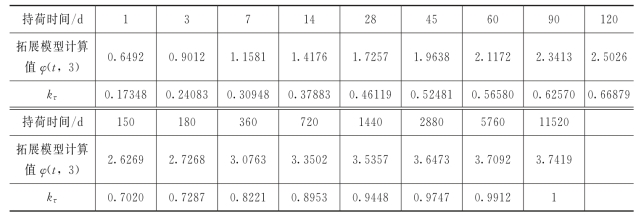
以拓展模型关于徐变系数的计算结果为基准建立了基本状态徐变系数数据样本。根据计算结果及工程经验的总结,近似以持荷时间11520d(30年)为徐变系数终值(此后徐变不再发生变化),以φ(t,3)/φ(11520,3)的比值作为持荷时间影响系数kτ,见表2.4。

表2.4　0～11520d持荷时间影响系数

用4种函数拟合图2.3曲线。

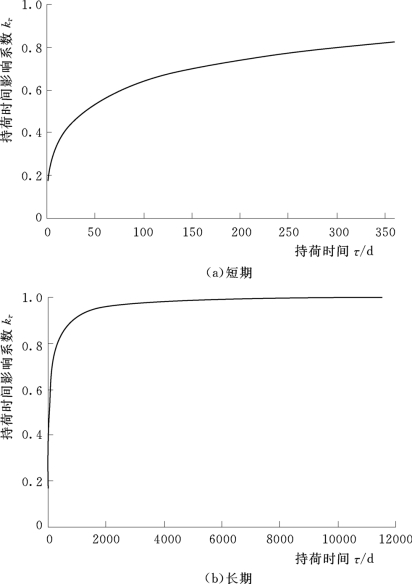
图2.3　持荷时间影响系数kτ曲线

方法1:设y=kτ,有Logatithmic(对数函数):y=a 0+a 1 lnτ。

方法2:Cubic(3次多项式):y=a 0+a 1τ+a 2τ2+a 3τ3+…。

方法3:结合数据特点设计公式:

方法4:采用指数函数形式,并结合数据特点设计公式:y=1-a exp(-bτ)。

用统计软件SPSS非线性回归的结果如下。

方法1的回归结果:y=0.205+0.098lnτ,RSq=0.956。

方法2的回归结果:在进行4次多项回归时,参数过多,进入死循环,RSq=0.800。(https://www.xing528.com)

方法3的回归结果: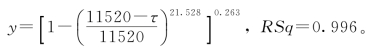

方法4的回归结果:y=1-0.72exp(-0.006τ),RSq=0.953。

RSq为回归的相关系数的平方值,它是衡量模型回归优越性能的指标,RSq越接近1则模型越优越。对上述4个模型进行比较,第三个模型的RSq最大,接近1,说明回归拟合的效果最好,但为了随后的有限元计算中避免应力历史的存储,在此利用方法4的回归结果。持荷时间影响系数kτ曲线如图2.3所示。通过上述分析,最终得到基本状态下,徐变系数计算的基本方程为:

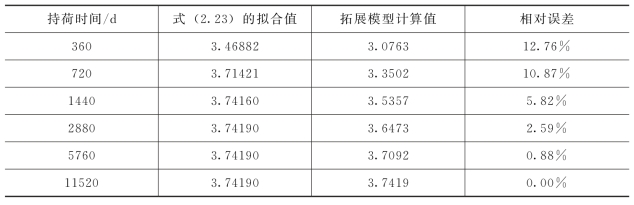
通过拟合公式(2.23)得到基本状态徐变系数的数据样本,并与拓展模型计算值比较,见表2.5。

表2.5　基本状态徐变系数数据样本

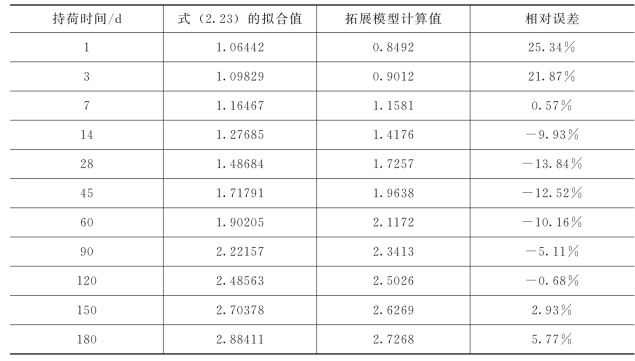
续表

从图2.3可以看出,混凝土徐变变形初始增长都很快,慢慢趋于平稳。徐变系数在0～360d发展迅速,并逐渐趋于恒定。根据拟合公式的计算,在持荷11520d(30年)以后,徐变系数的5位有效数字保持不变。为了直观地表示徐变系数发展速率,以基本状态下持荷11520d(30年)为徐变系数的最终值,把几部分持荷时间内的徐变系数的增量与徐变系数的最终值相比较,得到徐变系数的持荷时效比重示意图,如图2.4所示。

图2.4　徐变系数的持荷时效比重示意图

从图2.4可以看出,徐变系数在持荷时间28d内的增量比重最大、增长速度最快,达到徐变系数终值的45%;在持荷时间0～360d内,徐变系数的增量总和达到徐变系数终值的81%;在持荷时间τ→11520d(30年)时,徐变系数增量Δφ→0。