弹性单桩内力和位移分析计算-土力学与地基基础

确定单桩水平承载力特征值有分析计算和水平静载实验两种途径。分析计算法根据某些假定而建立理论（如弹性地基梁理论），计算桩在水平荷载作用下，桩身内力与位移及桩对土的作用力，验算桩身材料和桩侧土的强度与稳定及桩顶位移等，从而可评定桩的水平承载力特征值。

1.文克尔地基模型与弹性地基梁

文克尔地基模型由文克尔（E.Winkler）于1867年提出。该模型假设地基土表面上任一点处的变形is与该点所受的压力强度ip成正比，而与其他点上的压力无关，即

式中　C——地基抗力系数，也称地基系数（kN/m3）。

文克尔地基模型把地基视为刚性基座上由一系列侧面无摩擦的土柱组成，并可以用一系列独立的弹簧来模拟，如图8.16所示。其特征为地基仅在荷载作用区域下发生与压力成正比例的变形，在区域外的变形为零。基底反力分布图形与地基表面的竖向位移图形相似。显然当基础的刚度很大，受力后不发生挠曲，则按照文克尔地基的假定，基底反力成直线分布，如图8.16所示。受中心荷载时，则均匀分布。将设置在文克尔地基上的梁称为弹性地基梁。

图8.16　文克尔地基模型示意图

2.桩的弹性地基梁解法

桩顶受到轴向力、水平力和弯矩时，如果略去轴向力影响，桩就可以看作一个设置在弹性地基中的竖梁（若作用于杆的力或弯矩均与杆的轴线相垂直，并使该杆发生弯曲，这个杆就称为梁）。求解其内力的方法有三种：① 用数学方法解桩在受荷后的弹性挠曲微分方程，再从力的平衡条件求出桩各部分的内力位移（这是当前广泛采用的一种）；② 将桩分成有限段，用差分式近似代替桩的弹性挠曲微分方程中各阶导数式而求解的有限差分法；③ 将桩划分为有限单元的离散体，然后根据力的平衡和位移协调条件，解得桩各部分内力和位移的有限元法。本书介绍第1种。弹性地基梁解法从土力学观点认为是不严密的，但由于概念明确，方法简单，结果偏安全，在国内外使用较为普遍。我国公路、铁路、水利在桩的设计中常采用“m”法、“K”法、“C值”法、“常数”法等都属于此种方法。

3.地基系数分布规律

地基系数C值可通过各种实验方法取得，如可以对试桩在不同类别土质及不同深度进行实测xz及pzx后凡算得到。大量实验表明，地基系数C值不仅与土的类别及其性质有关，而且也随着深度而变化。由于实测客观条件和分析方法不尽相同等原因，所采用C值随深度的分布规律也各不相同。目前国内采用的地基系数分布规律的几种不同图示如图8.17所示。

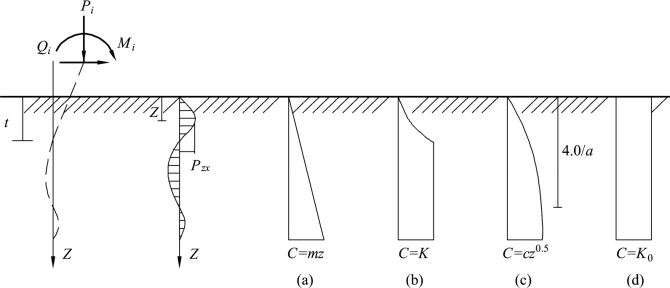
图8.17　地基系数变化规律

1）“m”法

假定地基系数C值随深度成正比例增长，即C＝mz，如图8.17（a）所示。m称为地基比例系数（kN/m4）。

2）“K”法

假定桩身挠曲曲线第一挠曲零点（即图8.17所示深度t处）以上，地基系数C随深度增加呈凹形抛物线变化；在第一挠曲零点以下，地基系数C=K（kN/m3），不再随深度变化而为常数[图8.17（b）]。

3）“C值”法

假定地基系数C随着深度成抛物线规律增加，即C＝cz0.5，如图8.17（c）所示。c为地基土比例系数（kN/m3.5）。

4）“常数”法（又称张有龄法）

假定地基系数C沿深度均匀分布，即C＝K0（kN/m3）为常数，如图8.17（d）所示。

上述四种方法均为按文克尔假定的弹性地基梁法。实测资料分析表明，对桩的变位和内力主要影响为上部土层，故宜根据土质特性来选择恰当的计算方法。对固结黏土和地面为硬壳层的情况，可考虑使用“常数”法；对于其他土质一般可用“m”法或“C”法；当桩径大、容许位移小时宜选用“C”法。“K”法误差较大，现较少采用。

4.水平荷载作用下的竖直桩

考虑一长度为l的桩，在桩顶（即z=0）作用有水平集中力H0和弯矩M0，如图8.18（a）所示。图8.18（b）给出了桩的扰曲变形和反力，图8.18（c）为扰度、截面转角、弯矩、剪力和土水平抗力的正号规定。

根据简化文克尔模型，将弹性介质（此时为土）视为一系列不相联系的无限接近的弹簧。

式中　k ——土的水平抗力系数（kN/m2）；

p ——土的水平抗力（kN/m）；

x ——扰度（m）。

图8.18　水平荷载作用下的竖直桩（Braja M.Das，1990）

1）砂性土

对砂性土，水平抗力系数kz随深度z线性变化，即

式中　m ——水平抗力系数的比例常数（kN/m3）。

参照图8.18（b），采用弹性地基梁理论得，

式中　Ep——桩材的弹性模量（kPa）；

Ip——桩截面的惯性矩（m4）。

基于文克尔模型

式（8.11）中的负号是因为土的反力与桩的变形方向相反，将其代入式（8.10）得

根据图8.18（b）的边界条件，可求得微分方程（8.12）的特解，即任意截面z处的扰度、转角、弯矩、剪力和土水平抗力

扰度

转角

(www.xing528.com)

弯矩

剪力

反力

式中　Ax，Bx，Aθ，Bθ，mA，mB，vA，Bv，pA和pB为与z有关的系数，且特征长度

当桩长l≥5α时，认为是长桩；桩长l≤2α时，认为是刚性桩。表8.7列出了长桩情况各个系数值。表中的第一列Z为无量纲深度

表8.7　长桩的系数（Braja M.Das，1990）

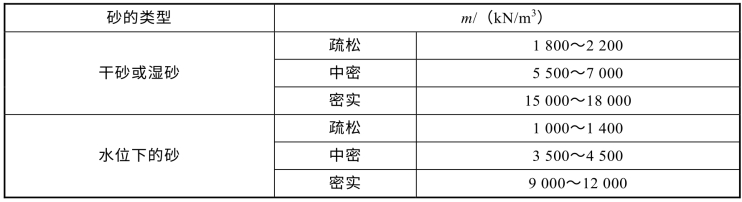
表8.8给出一些典型砂土的m值。

表8.8　砂土的m值（Braja M.Das，1990）

2）黏性土

对于埋入黏性土中的桩，类似于微分方程（8.12）的解法得

扰度

弯矩

式中为系数，且

图8.19给出了式（8.20）和（8.21）中的系数值，图中

图8.19　系数随Z的变化（Braja M.Das，1990）

采用式（8.20）和（8.21）时，必须知道特征长度R的值。如果已知水平抗力系数k，可由式（8.22）得知R值。对砂性土，水平抗力系数k随深度线性变化，而在黏性土中，水平抗力系数k近似的认为不随深度变化，可由下式计算

式中　0E——土的变形模量，黏土的变形模量为（1～30）×103kPa；

d——桩截面宽度或桩径（m）；

μ——土的泊松比，其值在0.3到0.4之间。

根据上面的理论分析和计算公式可知，当给定土的特性指标，桩的材料、长度和截面尺寸，就可以从桩顶的允许水平位移x0和桩身允许承担的弯矩Mz计算桩顶的允许水平荷载H0和M0。下面以砂性土中的钢桩为例说明怎样用桩顶的允许水平位移x0确定允许水平荷载H0（《地基基础规范》称其为水平承载力特征值，记为RHa）。

【例题8.3】有一个长25 m的H型钢桩打入砂性土中，已知钢桩的截面高度d1＝0.254m，截面模量Ip＝123×10-6m4，弹性摸量Ep＝207×106kN/m2，钢材的允许应力σa＝125N/mm2，桩顶的允许位移为8 mm，假定M0＝0，取水平抗力系数的比例常数m=12 000 kN/m3，计算允许水平荷载H0（引自：Braja M.Das，1990）。

【解】

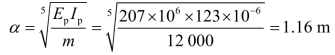
l/α＝25/1.16＝21.55>5，故为长桩。因为M0＝0，得

已知：xz(z＝0)＝8mm＝0.008m，z＝0时，Ax＝2.435（表8.7）

以上H0值是基于桩顶允许位移得到的，还需计算基于弯矩承载力的H0值。由式（8.15）当M0＝0时

Mz＝AmH0α

据表8.7，任意深度mA的极大值等于0.772，桩的最大允许弯矩等于

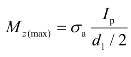
代入已知数据得

取H0＝53.6kN。

一般用公式计算水平承载力特征值仅是初步估计，更为准确的方法是横向静载荷试验。我国《地基基础规范》也规定，单桩水平承载力取决于桩的材料强度、截面刚度、入土深度、土质条件、桩顶水平位移的允许值和桩顶嵌固情况等因素，应通过现场水平载荷试验确定。