软弱下卧层承载力验算

在多数情况下，随着深度的增加，同一土层的压缩性降低，抗剪强度和承载力提高。但在成层地基中，有时却可能遇到软弱下卧层。如果在持力层以下的地基范围内，存在压缩性高、抗剪强度和承载力低的土层，则除按持力层承载力确定基底尺寸外，尚应对软弱下卧层进行验算。要求软弱下卧层顶面处的附加应力设计值zσ与土的自重应力σcz之和不超过软弱下卧层的承载力设计值fz，即

式中　zσ——相应于荷载效应标准组合时，软弱下卧层顶面处的附加应力值；

σcz——软弱下卧层顶面处土的自重应力值；

fz——软弱下卧层顶面处经深度修正后的地基承载力（kPa）。

计算附加应力zσ时，一般按压力扩散角的原理考虑（图7.18）。当上部土层与软弱下卧层的压缩模量比值大于或等于3时，zσ可按下式计算：

条形基础

矩形基础

式中　p——基础底面平均压力设计值（kPa）；

σcd——基础底面处土的自重应力（kPa）；

b——条形和矩形基础底面宽度（m）；

l——矩形基础底长度（m）；

z——基础底面至软弱下卧层顶面的距离（m）；

θ——地基压力扩散线与垂线的夹角（°），按表7.5采用。

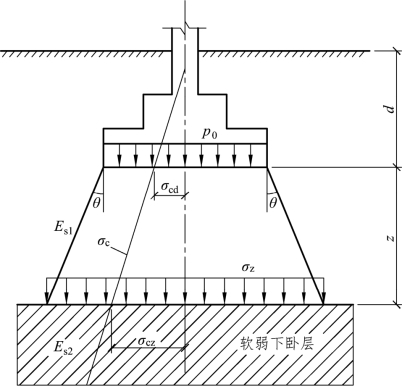
图7.18　软弱下卧层承载力验算

表7.5未列出的资料。对此，可认为：当时，意味着下层土的压缩模量与上层土的压缩模量差别不大，即下层土不“软弱”。如果Es1＝Es2，则不存在软弱下卧层了。

表7.5同时适用于条形基础和矩形基础，两者的压力扩散角差别一般小于2°。当基础底面为偏心受压时，可取基础中心点的压力作为扩散前的平均压力。

表7.5　地基压力扩散角θ

注：①Es1为上层土的压缩模量；Es2为下层土的压缩模量。
② z＜0.25b时一般取θ=0，必要时，宜由试验确定；z≥0.50b时θ值不变。

如果软弱下卧层的承载力不满足要求，则该基础的沉降可能较大，或者可能产生剪切破坏。这时应考虑增大基础底面尺寸，或改变基础类型，减小埋深。如果这样处理后仍未能符合要求，则应考虑采用其他地基基础方案。

【例题7.2】如图7.19中的柱下矩形基础底面尺寸为5.4 m×2.7 m，试根据图中各项参数验算持力层和软弱下卧层的承载力是否满足要求。

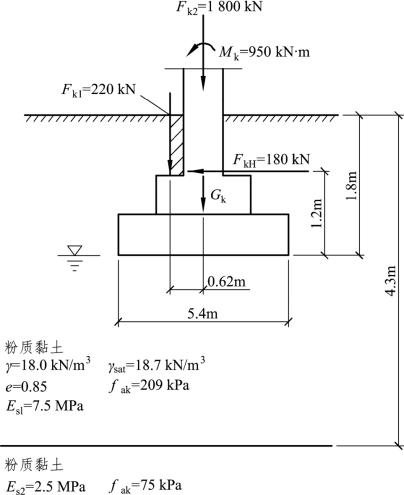
图7.19　例题7.2柱下矩形基础(www.xing528.com)

【解】（1）持力层承载力验算。

先对持力层承载力特征值fa进行修正。查表7.4，得ηb=0，ηd=1.0，则

fa＝209+1.0×18×(1.8-0.5)＝232.4kPa

基底处的总竖向力：

Fk＝+Gk＝1800+220+20×2.7×5.4×1.8＝2545kPa

基底处的总力矩：

Mk＝950+180×1.2+220×0.62＝1302kN∙m

基地平均压力：

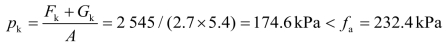
满足要求。

偏心距：

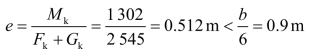
满足要求。

基底最大压力：

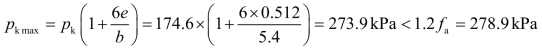
满足要求。

（2）软弱下卧层承载力验算。

下卧层顶面处的附加应力：

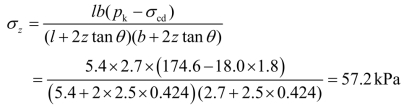
下卧层顶面处的自重应力：

σcz＝18.0×1.8+(18.7-10)×2.5＝54.2kPa

下卧层承载力特征值：

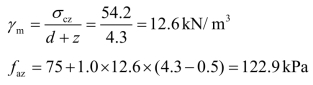
验算：

σcz+σz＝54.2+57.2＝111.4kPa<f az

满足要求。

经验算，基础底面尺寸满足持力层与软弱下卧层承载力要求。