简化土坡稳定分析-土力学与地基基础

1.无黏性土坡稳定性分析

无黏性土没有黏聚力，因此，只要土坡坡面上各个土粒不滑动，土坡就能保持稳定。取坡面的土粒为脱离体，分析其处于极限平衡状态时的条件（图6.18）。

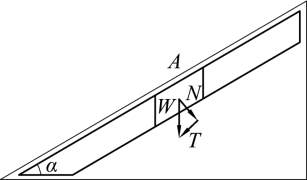
图6.18　无黏性土坡稳定分析

设土粒M重量为W，砂土的内摩擦角为φ，则土粒的重量W在垂直和平行于坡面方向的分力分别为

N＝Wcos β

T＝Wsin β

分力T是下滑力，它将使土粒M向下滑动，而阻止土粒下滑的抗滑力则是由垂直于坡面的分力N引起的摩擦力T′

T′＝Ntanφ＝Wcosβtan φ

则稳定安全系数

由上式可知，当坡角β等于土的内摩擦角φ时，K=1，则土坡处于极限平衡状态，稳定坡角β等于土的自然休止角，只要β＜φ（K＞1），土坡就能稳定，与坡高H无关。一般可取K=1.1～1.5，就能满足无黏性土坡的稳定要求。

2.黏性土坡稳定性分析

1）瑞典圆弧法

瑞典圆弧滑动法，又称整体圆弧法，是由瑞典的彼得森于1915年提出，广泛用于实际工程，是条分法中最古老而又最简单的方法，是极限平衡法的一种常用分析法。该法假定土体滑动面呈圆弧形，并不考虑条块间有力的作用。瑞典圆弧滑动法常用于边坡或土坡的稳定性。

瑞典圆弧滑动法是指均质黏性土坡滑动时，其滑动面常近似为圆弧形状，假定滑动面以上的土体为刚性体，即设计中不考虑滑动土体内部的相互作用力，假定土坡稳定属于平面应变问题，如图6.19。圆弧滑动法是最常用的边坡稳定极限分析方法，因其方法简单，通过极限平衡法就能直接得出安全系数，且在确定强度指标及选取合适的安全系数方面积累了不少经验。

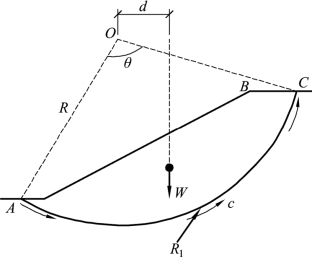
图6.19　瑞典圆弧滑动法

通常取圆弧滑动面以上滑动体为脱离体，土体绕圆心O下滑的滑动力矩为Ms，阻止土体滑动的力是滑弧AC上的抗滑力，其值等于土的抗剪强度τf与滑弧AC长度L的乘积，其抗滑力矩为Mr。安全系数：

2）瑞典条分法

瑞典条分法又称为费伦纽斯（Fellenius，1927）法，该法假定土坡沿着圆弧面滑动，并认为土条间的作用力对土坡的整体稳定性影响不大，可以忽略（由此而引起的误差一般为10%～15%），即假定相邻土条两侧的作用力大小相等、方向相反且作用于同一直线上。

把滑动土体分为若干条土条后，如图6.20所示，作用在条i的力，除重力iW外，土条侧面ac和bd作用有法向力iP，Pi1+，切向力Hi，Hi+1，法向力的作用点距弧面cd两端的高度分别为ih，hi+1。滑弧段cd的长度为li，其上作用着法向力Ni和切向力iT，iT中包括黏聚阻力和摩擦阻力。

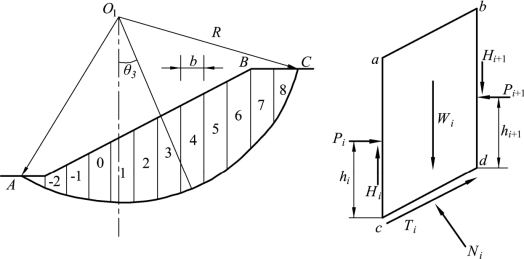
图6.20　瑞典条分法

如图6.21所示，取条块i进行分析，土条自重为Wi，土条底部的正压力为Ni＝Wicosθ i，土条底面上的抗剪力，方向则与滑动方向相反。当土坡处于稳定状态（Fs＞1）并假定各土条底部滑动面上的安全系数均等于整个滑动面上的安全系数时，则实际发挥的抗剪力为：，滑动土体内各土条对圆心O取力矩平衡条件：。可得：

图6.21　条块i分析图

3）简化毕肖浦法

毕肖普法是条分法的一种，假定滑动面是一个圆弧面，考虑土条侧面的作用力，并假定各土条底部滑动面上的抗滑安全系数均相同，即等于整个沿动面的平均安全系数。

通过每一条土条的静力平衡状态，根据竖向力平衡条件，应有：

Wi+ΔHi＝Nicosθi+Tisinθi

Nicosθi＝Wi+ΔHi-Tisin θi

根据满足安全系数为Fs时的极限平衡条件：

整理可得：

考虑整个滑动土体的整体力矩平衡条件，各土条的作用力对圆心力矩之和为零。这时条间力Pi和Hi成对出现。大小相等，方向相反，相互抵消，对圆心不产生力矩。滑动面上的正压力Ni；通过圆心，也不产生力矩。因此，只有重力Wi和滑动面上的切向力Ti又对圆心产生力矩。由整体力矩平衡得：(www.xing528.com)

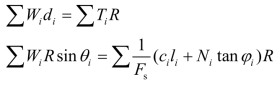
简化后得：

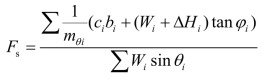
这就是毕肖甫法的土坡稳定一般计算公式。式中ΔH=Hi+1-Hi仍然是未知量。毕肖甫进一步假定ΔH=0，实际上也就是认为条块间只有水平作用力Pi而不存在切向力Hi，于是上式进一步简化为：

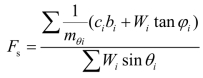
试算时，可先假定Fs＝10，由上式计算出各miθ所相应的值。代入式中，求得边坡的安全系数。若于sF之差大于规定的误差，用计算miθ，再次计算出安全系数，如此反复迭代计算，直至前后两次计算的安全系数非常接近，满足规定精度的要求为止。通常迭代总时收敛的，一般只要3到4次就可以达到精度要求。简化毕肖浦法见图6.22。

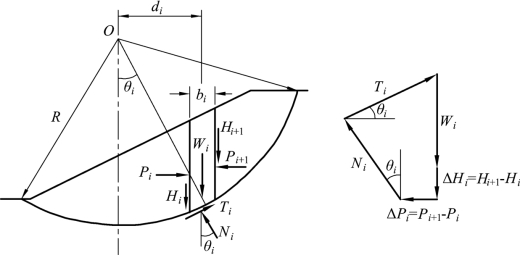
图6.22　简化毕肖浦法

4）确定最危险滑动面圆心的方法

边坡稳定分析中，因为滑动面是任意取的。假设一个滑动面，就可计算其相应的安全系数。真正代表边坡稳定程度的安全系数是安全系数中的最小值。相应于最小的安全系数的滑动面称为最危：险滑动面，它才是真正的滑动面。

确定最危险滑动面圆心的位置和半径大小是稳定分析中十分烦琐的工作。需要通过多次的计算才能完成。费伦纽斯（W.Fellenius）提出了最危险滑动面确定的经验方法。费伦纽斯认为，对于均匀黏性土坡，最危险滑动面一般通过坡脚，如图6.23。

图6.23　最危险滑动圆心的确定方法

对于φ＝0的土，最危险滑动面的圆心位置可以由AO与BO的交点确定。

对于φ﹥0的土，最危险滑动面的圆心位置，可能在DE延长线上。

当土的内摩擦角φ＝0时，土坡的最危险圆弧滑动面通过坡脚，然后由坡角β或坡度1∶n查表6.1可得出角β1以及β2。过坡脚B和坡顶C分别作与坡面和水平面夹角为β1、β2的线BD和CD，得交点D即为最危险滑动圆弧圆心（见图6.24）。

表6.1　1β、2β表

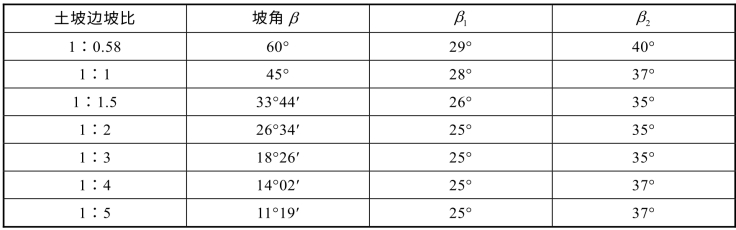
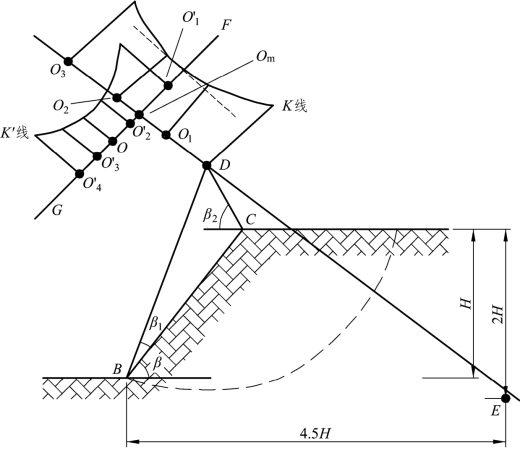
图6.24　确定最危险滑动面圆心位置

并不是最危险滑动面的圆心，这时可以通过Om点作DE线的垂线FG，在FG上取几个试算滑动面的圆心O1′，O2′，…，求得其相应的滑动稳定安全系数K1′，K2′，…，绘得K′ 值曲线，相应于K′min值的圆实际上土坡的最危险滑动面圆心位置有时并不一定在ED的延长线上，而可能在其左右附近，因此圆心Om可能心O才是最危险滑动面的圆心。

思考题

6.1　土压力的分类。

6.2　土压力的两种古典计算方式的区别。

6.3　分别指出下列变化对主动土压力和被动土压力各有什么影响？

（1）内摩擦角变大。

（2）外摩擦角变小。

（3）填土面倾角增大。

（4）墙背倾斜（俯斜）角减小。

6.4　为什么会发生边坡失稳？

6.5　举例说明影响土坡稳定的因素有哪些。

6.6　位于稳定土坡坡顶上的建筑物，如何确定基础底面外边缘线至坡顶边缘线的水平距离？

习题

6.1　墙背垂直光滑的挡土墙，墙高5 m，墙后填土为无黏性土，填土表面水平。填土γ＝18kN/m3，φ＝40°，c＝0。试分别计算出静止土压力、主动土压力、被动土压力。若墙于土间的摩擦角δ＝20°，试求主动土压力。

6.2　试计算图6.25所示地下室外墙上的土压力分布图、合力大小及其作用点位置。

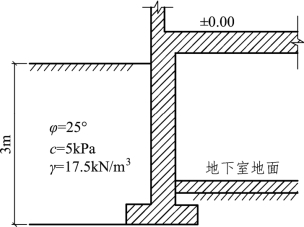
图6.25　习题6.2图

6.3　土坡高度为8 m，土的内摩擦角φ＝10°（Ns=9.2），c=25 kPa，γ＝18kN/m3的土坡，试计算其稳定安全系数。