主动土压力分析-土力学与地基基础

考察挡土墙后主体表面下深度z处的微小单元体的应力状态变化过程。当挡土墙在土压力的作用下向远离土体的方向位移时，作用在微分土体上的竖向应力zσ保持不变，而水平向应力xσ逐渐减小，直至达到土体处于极限平衡状态。土体处于极限平衡状态时的最大主应力为σ1＝γz，而最小主应力σ3即为主动土压力强度pa。根据土的极限平衡条件，可推导出主动土压力强度ap的计算公式如下：

无黏性土

黏性土

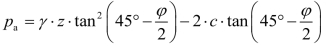
或

式中　Ka——主动土压力系数，Ka＝tan2。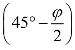

主动土压力分布规律：

由朗肯主动土压力计算公式可知，无黏性土中主动土压力强度pa与深度z成正比，沿墙高的土压力强度呈三角形分布（如图6.7）。作用在单位长度挡墙上的土压力为三角形分布面积，即

土压力作用点在距墙底h/3高度处。

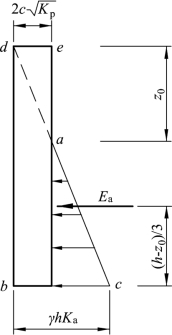
黏性土中的土压力强度由两部分组成：一部分是由土体自重引起的土压力γzKa，另一部分是黏力c引起的负侧压力，两部分的叠加结果如图6.8所示，其中aed部分是负侧压力，对墙背是拉应力，但实际上土与墙背在很小的拉应力作用下即会分离，故在计算土压力时，这部分的压力应设为零，因此粘性土的土压力分布仅是abc部分。令式（6.2）为零即可求得临界深度z0：

单位长度挡墙上的主动土压力可由土压力实际分布面积计算（图6.8中abc部分的面积）。主动土压力E0的作用点通过三角形的形心，即作用在离墙底高度处。

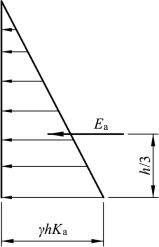
图6.7　无黏性土的pa分布

(www.xing528.com)

图6.8　黏性土的pa分布

朗肯主动土压力计算的具体方法可查阅例题6.1。

【例题6.1】有一挡土墙高6 m，墙背竖直、光滑，墙后填土面水平，填土的物理力学指标为：c =15 kPa，φ=15°，γ =18 kN/m3。求主动土压力及其作用点并绘出主动土压力分布图。

【解】（1）计算墙顶处的主动土压力强度pa1。

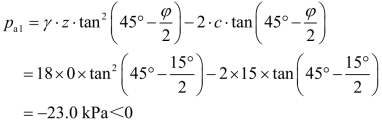
（2）计算临界深度z0。

（3）计算墙底处的主动土压力强度pa2。

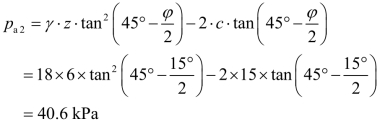
（4）绘出主动土压力的分布图如图6.9所示。

（5）计算主动土压力值。

主动土压力值按分布面积计算如下：

（6）计算Ea的作用点位置。

主动土压力Ea的作用点离墙底的距离为：

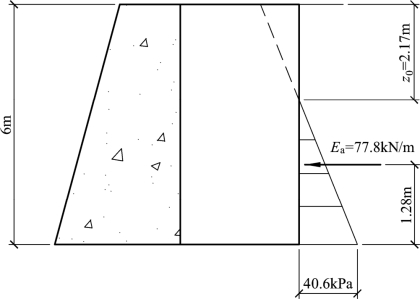
图6.9　例题6.1土压力分布图