普朗特公式的实用性-土力学与地基基础

1920年，L.普朗特（Prandtl）根据极限平衡理论，研究刚性冲模压入无质量的半无限刚塑性介质时，导出了介质达到破坏时的滑动面形状和极限压应力公式，人们把他的解应用到地基极限承载力的课题。

考虑受条形均布竖向荷载作用的底面光滑的条形刚性板置于无重量（γ=0）的均质地基表面上（d=0），地基材料具有刚塑性性质。当荷载板下的土体处于极限平衡状态时，滑动面形状如图4.13所示。

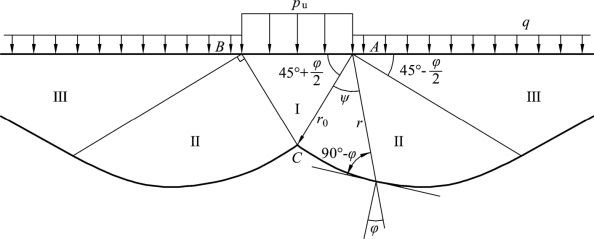
图4.13　均布竖向荷载作用下的塑性区

塑性区共分五个区，即一个I区，两个Ⅱ区和两个Ⅲ区。

I区——位于基底（刚性条板）以下的中心楔体aab′称为主动朗肯（Rankine）区。因基底光滑，即基础底面与土之间无摩擦力存在，则水平面（aa′面）为大主应力面，竖直面为小主应力面。破裂面与水平面夹角成。

Ⅱ区——滑动线有两组，一组是对数螺旋线b（c或bc′），其曲线方程为r＝r0exp(θtanφ)（r0为起矢径，，另一组是以a′和a为起点的幅射线。

Ⅲ区——小主应力面是水平面，其破裂面与水平面成，称为被动朗肯区。

对于上述情况，普朗特得出极限承载力的理论解为

(www.xing528.com)

式中　Nc——承载力系数：

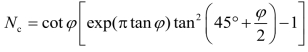
c，φ——土的黏聚力（kPa）和内摩擦角（°）。

实际上，基础一般都有一定埋深d，将基础底面以上两侧土体重量用均布超载q=γod代替图4.13所示。赖斯纳（Reissene，1924）在普朗特理论解基础之上提出地基极限承载力公式为

其中

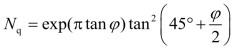
式中　Nc，Nq——承载力系数。

普朗特、赖斯纳得出的理论解是在特殊条件下得到的，实际地基土不是没有重量，基底与土之间也不是没有摩擦力的，也没有考虑基础埋深范围内侧面土的抗剪强度的影响，其结果与实际工程有较大差距。为此，许多学者在普朗特和赖斯纳理论解的基础上作出了修正和发展，提出各种不同的极限承载力近似计算方法，其中最典型的是以太沙基公式为代表的计算浅基础的极限承载力公式和梅耶霍夫提出的深基础极限承载力公式。下面分别对这两大类极限承载力公式加以介绍。