前已指出,地基土的变形通常要持续一段时间才能完成,变形稳定所需的时间与地基土的性质、排水条件等有关。碎石土和砂土地基,因透水性大,压缩性小,变形所经历的时间很短,可以认为在施工完毕时已经固结稳定;而黏性土地基,因透水性水,压缩性大,完成固结所需的时间就较长,尤其是饱和的软黏土,往往需要几年甚至几十年才能固结稳定。因此,在工程设计中,对于黏性土和粉土地基,不但需要知道地基的最终沉降量,往往还需要知道沉降与时间的关系,以便组织施工顺序、控制施工速度以及确定采取必要的建筑措施(如考虑建筑物有关部分的预留净空或连接方法)。关于沉降与时间的关系,目前均以饱和土体单向固结理论为基础,下面介绍这一理论及其应用。
1.饱和黏性土的渗透固结
饱和黏性土在压力作用下,只有排出孔隙中的自由水,才能使其体积减小,产生压缩变形,这一过程称为饱和土的渗透固结。下面我们以土的固结模型来说明土固结的力学机理。
饱和土的单向固结模型为图3.14所示的带弹簧活塞的充水容器。整个模型表示饱和土,弹簧模拟土的骨架,活塞上的小孔模拟排水条件,则容器中的水相当于孔隙中的自由水,以u表示由外荷p在土孔隙水中引起的超静水压力,称为孔隙水压力;以σ′表示土骨架中产生的应力,称为有效应力。
现在来分析模型受压力p作用时,其内部的应力变化和弹簧的压缩过程,即土的固结过程。
当活塞上骤然施加压力p时(相当于加荷压时t=0),瞬间图[3.14(a)]容器中水来不及排出,此时弹簧尚未受力,压力全部由水承担。即:t=0时,u=p,σ′=0;其后,t>0[图3.14(b)]时,水在u的作用下,开始从活塞上的小孔中排出,活塞下降,弹簧受到压缩,随着水的不断排出,σ′逐渐增加,u逐渐减小。即:0<t<∞时,p=σ′+ u;最后[图3.14(c)],当u→0,水停止排出,活塞不再下降,此时(理论上t趋于∞),压力全部由弹簧承担。即:t→∞时,σ′=p,u=0。

图3.14 饱和土渗透固结的简单模型
由此可见,饱和土的渗透固结是孔隙水压力消散、逐渐转移为有效应力的过程,只有孔隙水压力u=0时,土的固结变形才能完全稳定。
2.单向固结理论
单向固结理论是以土体受到单向加荷,从而产生同向的渗透固结压缩这一基本力学模型为基础的。固结理论的目的在于求解土体中某点的孔隙水压力随时间和深度变化的规律,即u=φ(z, t)。
1)基本假定
太沙基提出固结理论时,做了如下假定:
(1)土是均质、各向同性的饱和体。
(2)土颗粒和水都是不可压缩的。
(3)土的压缩和水的渗流只沿竖直方向发生。
(4)土中水的运动服从达西定律。
(5)在渗透固结过程中,土的渗透系数k和压缩系数a均为常数。
(6)荷载是瞬时一次施加的。
2)单向固结微分方程及其解答
(1)微分方程的建立
考虑图3.15(a)所示最简单的情况。有一饱和黏土层,厚为H,表面有透水层,底面为不透水及不可压缩层。设该土层在自重应力作用下固结已完成,现该土层表面骤然施加连续均布荷载p0,则在土中引起的附加应力σz(=p0)沿深度均匀分布,即ab=ce=σz=p0。由于水只能向上渗流从表面排出,当排水固结开始后,表面的孔隙水压力立即降到零,而底面的孔隙水压力则降低很少,其任意深度处的孔隙水压力随z不同而变化,如ad表示某一时间t时,土中有效应力σ′与孔隙水压力u沿深度的变化曲线。随着时间的增长,曲线逐渐发生变化,如图3.15(a)中的虚线。由此可见,有效应力σ′和孔隙水压力u是时间t和深度z的函数。
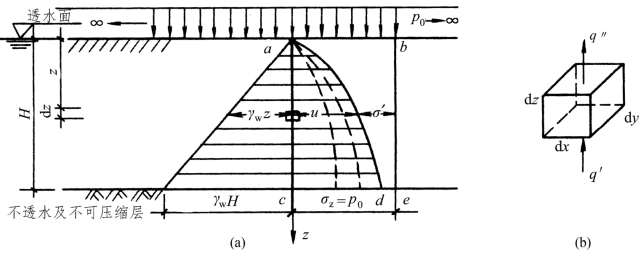
图3.15 饱和黏性土层的固结
设σ′=f(z,t),u=φ(z,t),显然当t=0时,σ′=f(z,0)=0,ad与be重合,u=φ(z,0)=σz,即σz全部由u承担;当t=∞时,u=φ(z,∞)=0,ad与ac重合,σ′=f(z,∞)=σz,即σz全部由土粒骨架承担。
从地基中任一深度z处取一微元土体dxdydz[图3.15(b)],已知其孔隙比为e时,微元体中土粒体积![]() ,孔隙体积
,孔隙体积![]() 。
。
由于水只能自下而上排出,故在单位时间dt内,以该微分体的水量变化为:
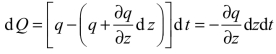
同时,由于土颗粒不能压缩,故在单位时dt内,微元体体积的变化等于孔隙体积的变化:
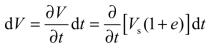
因在相同时间内,流经微元体的水量变化等于微元体体积的变化,即上两式相等,有:
![]()
式(3.29)为饱和土体单向渗透固结的基本关系式。
根据达西定律知:
![]()
则

根据土的压密定律知:
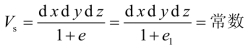
则
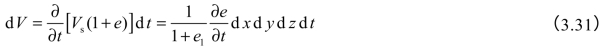
将上两式代入式(3.29)得:
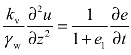
令
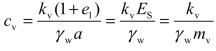
则
![]()
式中 kv——土的渗透系数[cm/s(1 cm/s≈3×105m/a)];
e——土固结前的初始孔隙比;
a——土的压缩系数(MPa-1);
γw——水的重度(10 kN/m3);
cv——土的竖向固结系数(m2/a)。
式(3.32)即为饱和土的单向固结分方程,根据不同的初始条件和边界条件,可用分离变量法求解。
(2)微分方程的解
现以图3.15为例来说明式(3.32)的一个特解。
初始及边界条件为
当t=0和0≤z≤H时,(加荷瞬间)u=σz;
t=∞和0≤z≤H时,(固结时土表面)u=0;
0<t<∞和z=H时,(不透水底面)∂u/∂z=0;
t=∞和0≤z≤H时,(固结完成)u=0。
根据上述条件,可得式(3.32)以富里埃级数表示的解为
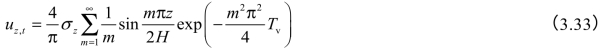
式中 m——正整奇数(1,3,5…);(https://www.xing528.com)
uz,t——某一时刻深度z处的超静水压力(kPa);
H——最大排水距离:当土层为单面排水时,H为土层的厚度;双面排水时,水由土层中心向上下同时排出,则H取土层厚度之半;
Tv——竖向固结时间因数。
![]()
3)固结度及其应用
(1)固结度
地基在固结过程中任一时间t的沉降量St与其最终固结沉降量S之比值Ut称为固结度,表示地基在t时所完成的固结程度。
![]()
由前面地基规范推荐的沉降计算公式推导中知,地基的变形沉降量等于有效附加应力面积除以压缩模量。则:

式中的孔隙水压力uz,t,视地基中的应力分布和排水条件不同而异,因而U-t关系亦不同,可根据不同情况下的初始及边界条件,对上式求解。现仍以图3.15(a)为例,将其解式(3.33)代入式(3.36)得:
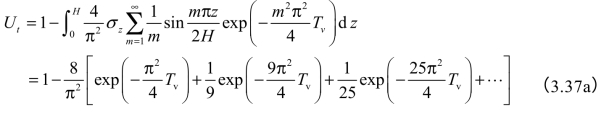
上式括号内的级数收敛很快,当U>30%时,可近似取其中第一项:

(2)几种固结情况
为了便于实际应用,根据不同的应力分布和排水条件,由式(3.36)可求解不同的Ut,图3.16所示不同v值的土层固结度与时间因素U-Tv的关系,称为渗透固结理论曲线。其中
![]()
前面分析的只是饱和单向排水地基受连续均布荷载作用,附加应力不随深度变化的情况,称之为情况0。一般对单向固结条件,可按v值不同分为如下5种情况:
情况0:v=1(pa=pb),适用于地基土在自重作用下已完成固结,基底面积较大而压缩土层较薄(H/b≤0.5)的情况。
情况1:v=0(pa=0),适用于大面积新填土由自重应力引起的固结,或土层因地下水位大幅度下降,在地下水变化范围内,自重应力随深度增大的情况。
情况2:v=∞(pb=0),适用于地基土在自重作用下已完成固结,基底面积较小而压缩土层较厚的情况。
情况3:v<1(pa<pb),适用于地基土在自重应力作用下尚未固结,又受到连续或局部荷载作用的情况。
情况4:v>1(pa>pb),适用于地基土在自重作用下已完成固结,但压缩土层不太厚,底在的附加应力仍相当大,不可视为零的情况。
以上所述均属单面排水情况,若为双面排水,则不论v为何种情况,其固结度都按情况0计算,但最大排水距离取土层厚度之半,即H/2。
(3)固结度的应用
当地基的固结情况为已知时,就可根据地基中应力的分布和排水条件,并利用图3.16关系曲线,解决下面两类问题:
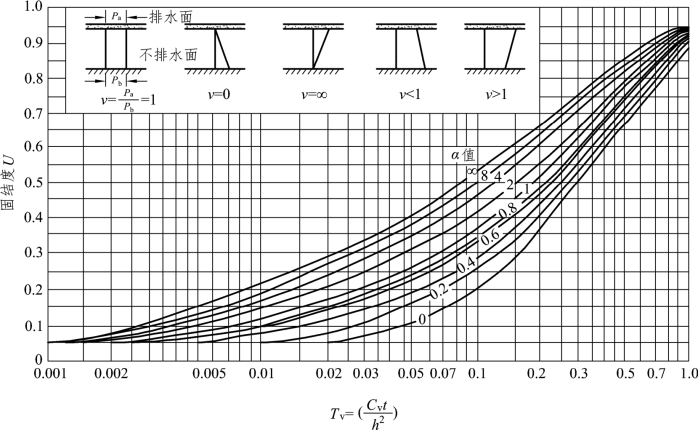
图3.16 U-Tv关系曲线
① 给定某固结历时t,求该历时的沉降量st。
解决这类问题,首先根据已知资料(地基的k、a、e、H和给定的t),算出土的竖向固结系数Cv和时间因数Tv,然后根据问题的固结情况,利用图3.16的关系曲线,查出相应的固结度U,再按式(3.35)求出t时的沉降量st。
② 给定固结度U,求达到该固结度所需的时间t。
解决这类问题,同样先按上述步骤算出固结系数Cv,然后按相应的情况,利用图3.16查出相应于U的时间因数Tv,再按式(3.34)求出时间t。
【例题3.4】设基础置于厚8 m的饱和黏土层上,其下为不透水的坚硬岩层,基底有砂透水层。已知地基附加应力分布为,其底处pa=140 kPa,岩面处pb=70 kPa,土层的初始孔隙比e0=0.85,压缩系数a=0.4 MPa-1(=4×10-4kPa-1),渗透系数k=0.59×10-7cm/s(≈0.018m/a)。试问:
(1)加荷1年后,基础沉降量为多少?
(2)需要多少时间,基础的沉降量可达155 mm?
(3)若饱和黏土层底面亦有一排水砂层,则上述两问题有何不同?
【解】(1)求t=1年时的基础沉降量。
土层的平均附加应力
![]()
则基础最终固结沉降量
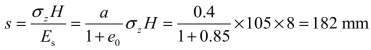
土的固结系数
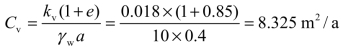
土层应力分布及排水条件属情况4。
时间因数
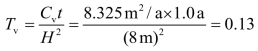
查图3.16得Ut=0.46。
则基础加荷1年后的沉降量:
st=Uts=0.46×182=83.7mm
(2)求st=155 mm时所需的时间。
土层固结度为![]()
查图3.16得Tv=0.65。
则需要时间为
![]()
(3)若黏土层底面有排水砂层时,即为双面排水情况,按情况0计算,即:v=1
当t=1年时,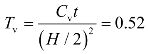
查图3.16得U=0.77。
加荷1年后的沉降量
st=Uts=0.77×182=140mm
当st=155mm 时,土层固结度为![]()
查图3.16得Tv=0.65。
所需时间 t=Tv(H/2)2/Cv=0.65×(8/2)2/8.325=1.25a
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




