土力学与地基基础：附加应力的竖向均布荷载效应

1.均布矩形荷载下的附加应力

当均布竖向荷载作用于矩形基础时，矩形基础角点下任一深度z处的附加应力可由布辛奈斯克公式进行积分求得。

在离坐标原点O为x、y处取一微分面积dA=dxdy，该面上集中力为dp（图2.12）。

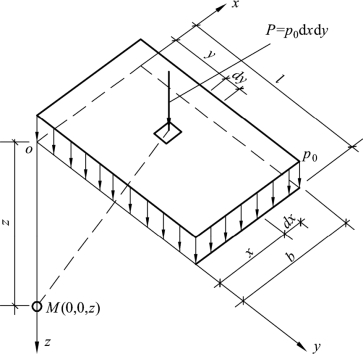
图2.12　均布矩形荷载角点下附加应力

由式（2.11）可得角点下M（0，0，z）的附加应力为

代入dp＝p0dzd y 及r2＝x2+y2，则

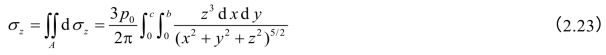
式中　A——基础底面面积，A=l·b；l为基础长边，b为基础短边；

p0——矩形基础上均布荷载。

通过积分得

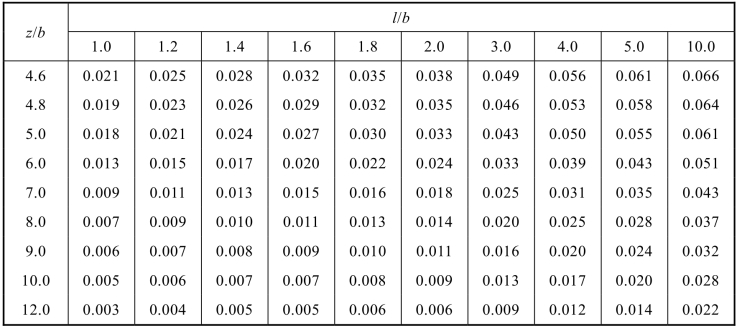
式中　αc——均布矩形荷载角点下附加应力系数，可查表2.6。

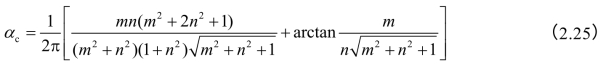
式中m=l/b，n=z/b。

表2.6　均布矩形荷载角点下的竖向附加应力系数αc

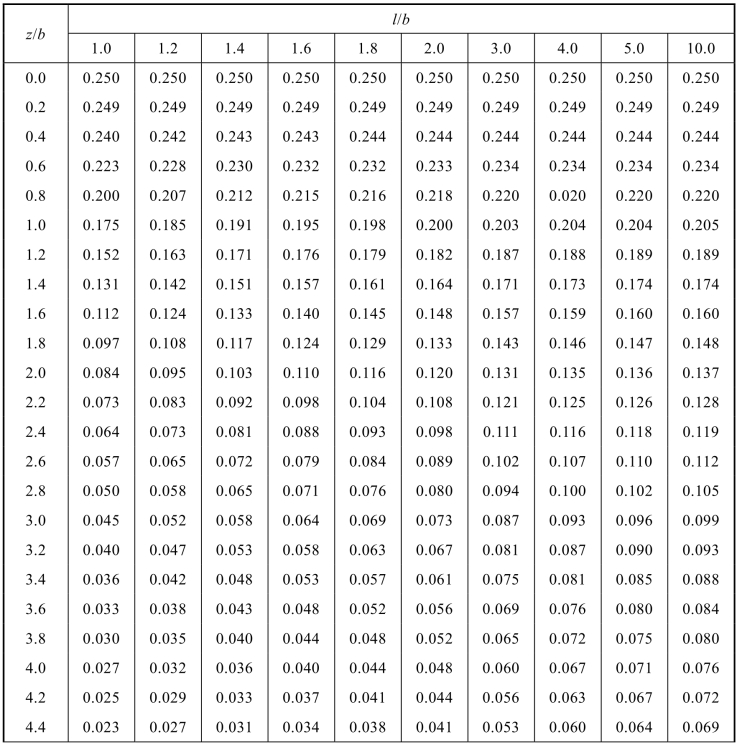
续表

2.角点法

当所求点不位于基础角点下时，可用角点法求解。通常M点的位置分下列三种情况。计算时，通过M点将荷载面积划分为若干个小矩形，然后按式（2.24）计算每个小矩形角点下同深度z处的附加应力，并求其代数和。注意若干个小矩形面积之代数和应等于基础原有的受荷面积。

（1）M点在荷载面边缘处[图2.13（a）]

σz(M)＝(αc+αc)p0

（2）M点在荷载面之内[图2.13（b）]

σz(M)＝(αc+αc+αc+αc)p0

（3）M点在荷载面边缘外侧[图2.13（c）]

σz(M)＝(αc-αc+αc-αc)p0

（4）M点在荷载面角点外侧[图2.13（d）](www.xing528.com)

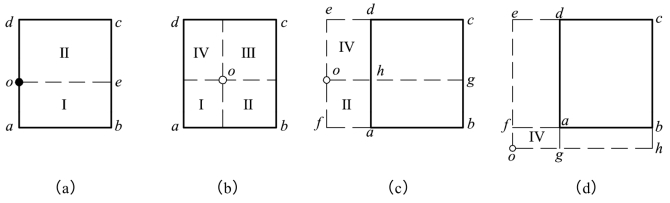
图2.13　角点法的应用

σz(M)＝(αc-αc-αc+αc)p0

【例题2.4】已知均布受荷基底面积如图2.14所示，求基底下8 m处M点的附加应力。p0=100 kPa。基底面积为3 m×2 m。

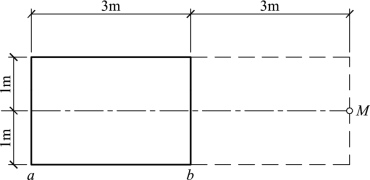
图2.14　例题2.4图

【解】σz＝2(αc(Ma)-αc(Mb))p0

l/b=6/1=6，z/b=8/1=8

查表1.2 αc(Ma)＝0.031 1

l/b=3/1=3，z/b=8/1=8

查表1.2 αc(Mb)＝0.0198

σz＝2(0.0311-0.0198)×100＝2.26kPa

3.三角形分布矩形荷载下的附加应力

设沿矩形基础一边b分布的三角形荷载最大值为pt，在三角形荷载范围内取一微分面积d A=dxdy，该面上集中力为（图2.15）。

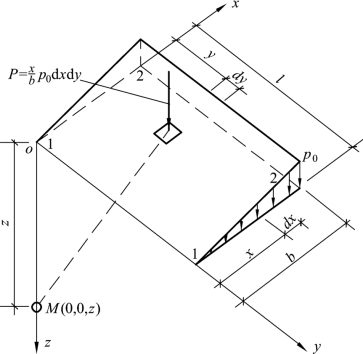
图2.15　三角形分布荷载角点下附加应力

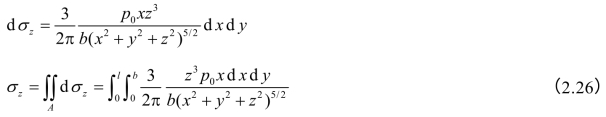
通过积分，得荷载为零值边的角点1下任意深度z处竖向附加应力为

σz＝αt1pt

式中

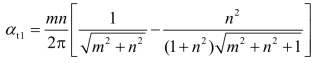
同理，还可求得三角形最大值边的角点2下任意深度z处的附加应力

σz＝αt2pt

αt1和αt2均为附加应力系数，且是m=l/b和n=z/b的函数，可以查表2.7得到。

表2.7　三角形分布矩形荷载角点下的竖向附加应力系数αt1和αt2

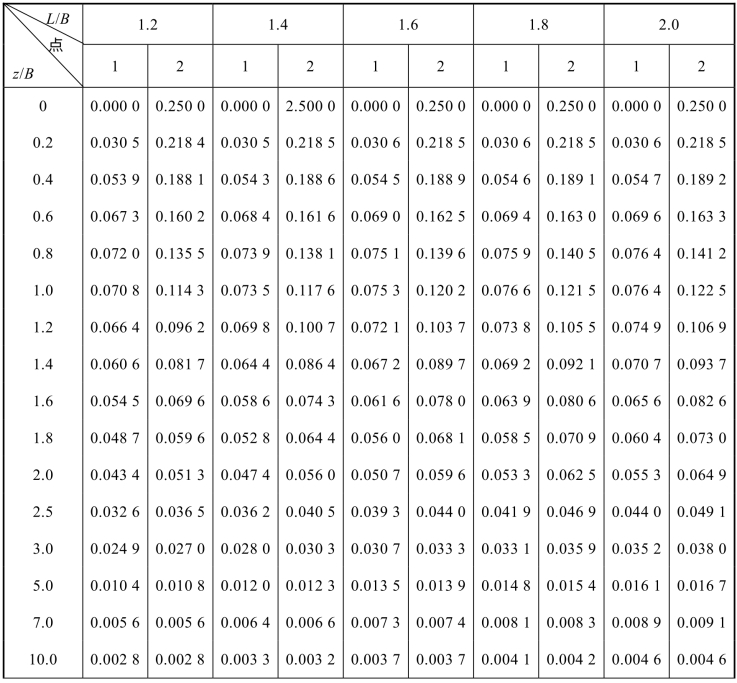
续表

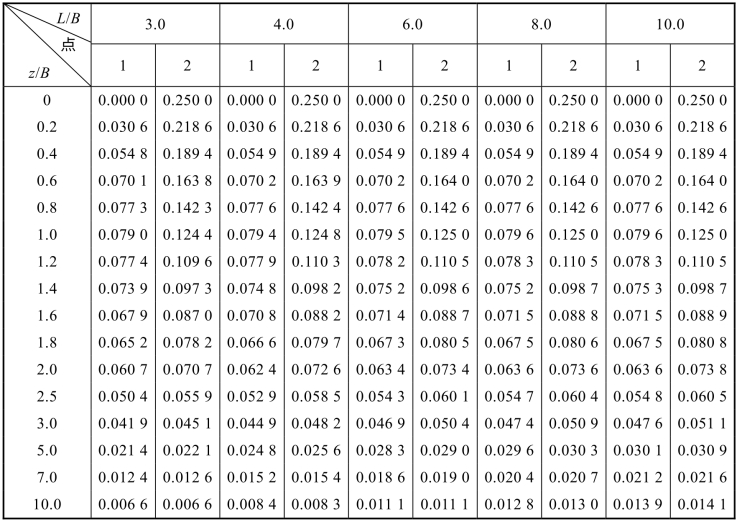
对于基底范围之内（或之外）任意点下的附加应力，仍可利用角点法和叠加原理来进行。但必须注意应使所求点位于三角形分布荷载为零（或最大值）一点垂线上，b始终指荷载变化方向矩形基础底面的长度。