铅直荷载下的附加应力影响-土力学与地基基础

垂直集中力P用在半无限直线变形体表面（相当于基础底面标高处水平面上）时，土中任意一点M（x，y，z）（图2.10）处的应力和位移解，已由法国布辛奈斯克（J.Boussineq，1885）求出，其表达式如下：

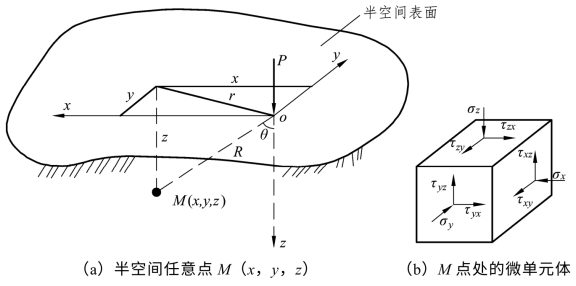
图2.10　半无限直线变形体在垂直集中力作用下的附加应力

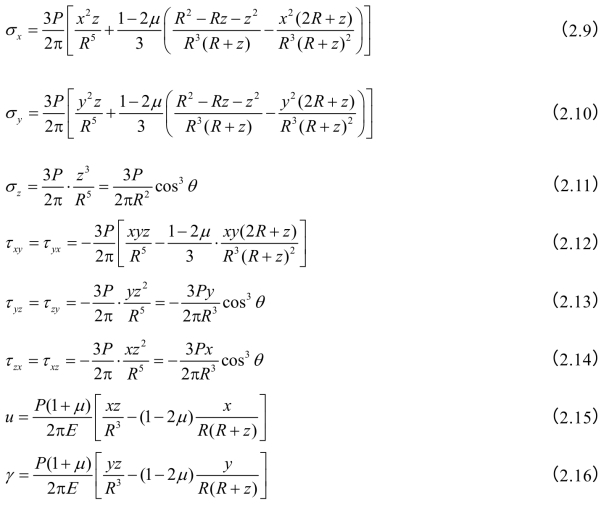
式中　σx，σy，σz——M点在x，y，z方向的法向应力；

τxy，τyz，τzx——剪应力，下角标的第一字母表示与剪应力作用面垂直的坐标，第二个字母表示与剪应力作用方向平行的坐标；

u，v，w——M点沿x，y，z方向的位移；

θ——z坐标与OM（R）的夹角；

E——弹性模量（或土力学中专用的地基变形模量，以E0代之）；

μ——土的泊松比；

R——M点距坐标原点O的距离。

当R=0，从以上算式得出的应力均为无穷大，表示该点附近已产生塑性变形，因此，所选择的计算点不应过于靠近集中力作用点。三个位移分量中最常用的是垂直位移分量w。由式（2.17），录z=0，R=r时，在距离集中力作用点为r处的垂直位移为

以上称布辛奈斯克解。其中使用最多的是应力分量zσ。式（2.1）可以改写如下形式：

式中　α——集中力作用下地基中附加应力系数，可按下式计算或查表2.1求得。

(https://www.xing528.com)

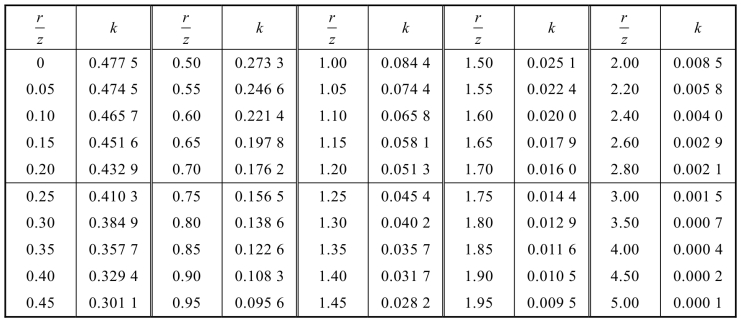
表2.1　集中力作用于空间表面时的竖向附加应力系数α

由式（2.19）和式（2.20）可知，当深度z不变时，即在同一水平面上，在集中力作用线上的附加应力比两侧的大。在集中力作用线上（r=0），附加应力随深度z增大而减小；在距作用线一定距离处，即r一定时，在地表处附加应力趋近于零，而后随深度有所增大，但至某一深度z开始，附加应力值随z增大而逐渐减小，这就是土中附加应力分布的扩散现象。

连接各深度的平面上附加应力相等的各点，便得到等值应力线图[如例图2.3（4）所示]。

【例题2.3】地面上作用着集中力P=100 kN，求：（1）当r=0时，z=1 m、2 m、3 m、4 m处的附加应力σz并绘出其分布图；（2）当r=2 m时，z=1 m、2 m、3 m、4 m处的附加应力σz并绘出其分布图；（3）当z=2 m，r=0、1 m、2 m、3 m、4 m处的附加应力σz及其分布图；（4）绘出σz=0.01P时的等应力线分布图。

【解】（1），（2），（3），（4）计算结果分别列于表2.2～2.5中。

表2.2　（1）计算结果（r=0）

α查表求得。

表2.3　（2）计算结果（r=2 m）

表2.4　（3）计算结果（z=2 m）

表2.5　（4）计算结果（σz=0.01P，α=0.01z2）

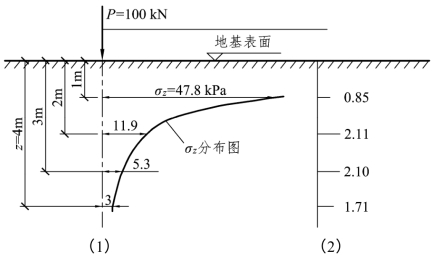
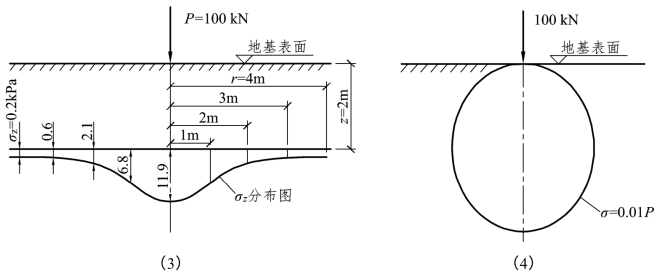
图2.11　例题2.3图