预测钢筋混凝土导热系数模型

本章3.1节所述的预测模型大多是用来计算两相复合材料的导热系数的，都有各自的优点和局限性。钢筋混凝土作为钢筋和混凝土组成的复合材料，应用哪种模型进行导热系数的估算更为准确，本节做了进一步研究。

（1）混凝土导热系数预测模型比较。

混凝土本身是一种复合材料，它主要由粗骨料、细骨料、水以及胶凝材料组成，其导热系数会受到这些组成材料的影响，但当组成其材料的性质和含量确定时，混凝土的导热系数也就基本确定。本节为研究钢筋混凝土的导热系数，采用相同组成成分的混凝土浇筑试件，仅改变混凝土中钢筋的用量和配置方式，可将钢筋混凝土看成是由混凝土和钢筋组成的两相复合材料，其中混凝土为连续相基体，钢筋为分散相粒子。但是在钢筋混凝土中，钢筋在混凝土中均匀并连续的分布，其分布是确定的而不具有随机性，因此不满足Maxwell模型、Bruggeman模型和Hamilton-Crosser模型的假定条件。热量在横向配筋的钢筋混凝土中的传递模型可以用来解释钢筋对混凝土导热系数的影响规律。在本试验中，钢筋在混凝土中均匀连续的分布，在不考虑钢筋和混凝土间的界面热阻时，可以用并联和串联模型来解释热量的传递规律。

实际上，复合材料组分之间界面的方向往往是随机分布的，在不考虑界面热阻的情况下，用串联模型和并联模型计算出来的等效导热系数对应于两相复合材料实际导热系数的上界和下界。因此，串联模型和并联模型可以用于估算配筋混凝土等效导热系数的大致范围。在模型建立时，近似认为同一截面上混凝土和钢筋为矩形单元。在本试验中，对比试验测试得到的混凝土的导热系数为1.43W/（m·K），而钢筋的导热系数为29W/（m·K）。图3.17给出了钢筋混凝土复合材料串联模型和并联模型等效导热系数随钢筋体积分数的变化规律。

图3.17　钢筋混凝土串联和并联模型等效导热系数随钢筋体积分数变化规律
Fig.3.17　Variation of equivalent thermal conductivity with rebar volume fraction in the series and parallel models

从图3.17中可以看出，无论是并联模型还是串联模型，钢筋混凝土的导热系数都随钢筋体积分数的增加而增大，与前述试验结果规律较为一致。并联模型中，由于混凝土和钢筋为两个互不干涉的热流通道，计算的导热系数偏大。串联模型中，钢筋和混凝土的热流通道相互衔接，混凝土相对钢筋来说，对热流产生了阻碍作用，计算的导热系数较小。在钢筋体积分数不断增长情况下，并联模型的导热系数增长幅度较大且均匀，串联模型的导热系数增长较慢，但当钢筋体积分数100%时，串联模型导热系数迅速增大到最大值。这表明在钢筋混凝土中，与钢筋相比。混凝土对热量的阻碍作用是非常明显的。

将并联和串联模型的计算值与试验值进行比较，如图3.18所示。可以看出，试验值落在串联和并联模型围成的区域内，且试验值更接近串联模型的计算值。在同一钢筋体积分数下，并联模型和串联模型的计算值相差较大，比如钢筋体积分数为2%时，并联模型和串联模型计算值相差了0.5W/（m·K）。

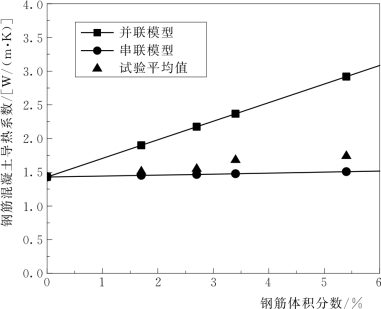
图3.18　钢筋混凝土导热系数试验值与并联模型和串联模型等效导热系数的比较
Fig.3.18　Comparison of test values and calculated equivalent thermal conductivity of parallel and series models

（2）不考虑界面热阻的串-并联模型和并-串联模型。

在钢筋混凝土试件中，钢筋竖向和水平向排列，四周被混凝土包裹。为了细化热量在钢筋混凝土中的传热模型，将并联模型和串联模型做进一步推广，得到串-并联模型和并-串联模型。

设混凝土的导热系数为λ1，体积分数为v1，钢筋的导热系数为λ2，体积分数为v2。在钢筋混凝土截面中，钢筋的实际截面为圆形，为便于模型的建立和保证计算结果的收敛性，将钢筋的实际截面按面积等效原则等效为正方形。也就是说，在等效代表单元中，钢筋的正方形截面面积等于钢筋原截面面积。在同一截面的等效代表单元中，将钢筋和混凝土都近似认为是正方形单元，v2=a2，那么a=。等效代表单元如图3.19所示。

串-并联模型如图3.20所示，先计算串联模型，根据串联模型计算式（3.7），则有

图3.19　模型的等效代表单元
Fig.3.19　Equivalent unit of models

图3.20　串-并联模型
Fig.3.20　series-parallel model

然后计算并联模型，根据并联模型计算式（3.8），则有

将式（3.29）代入并整理，得到串—并联模型等效导热系数计算公式

在并-串联模型（图3.21）中，先计算并联模型，根据并联模型计算式（3.8），则有

然后计算串联模型，根据串联模型计算式（3.7），则有

将式（3.32）代入并整理，得到并—串联模型等效导热系数计算公式(www.xing528.com)

图3.21　并-串联模型图
Fig.3.21　parallel-series model

图3.24给出了串-并联模型和并-串联模型中，钢筋混凝土导热系数随钢筋体积分数的变化规律。其中钢筋导热系数为29W/（m·K），混凝土导热系数为1.43W/（m·K）。从图3.22可以看出，两个模型中，钢筋混凝土导热系数随钢筋体积分数的增大而增大，但增加都较为平缓，仅从钢筋体积分数90%到100%的位置才显著增大。这是因为在两个模型中都考虑了混凝土对热量的阻隔作用。

在钢筋混凝土结构中，构件的综合配筋率（考虑受力钢筋和构造钢筋）一般最大可达10%，即钢筋最大体积分数可达10%。图3.23比较了并联模型、串联模型、串-并联模型和并-串联模型中钢筋混凝土导热系数随钢筋体积分数的变化规律，可以看出，串-并联模型和并-串联模型的导热系数计算值比并联模型和串联模型的导热系数计算值范围明显缩小，可以更加准确的估计钢筋混凝土的导热系数。

图3.22　串-并联模型和并-串联模型等效导热系数随钢筋体积分数变化规律
Fig.3.22　Variation of equivalent thermal conductivity with rebar volume fraction in series-parallel model and parallel-series model

图3.23　钢筋混凝土导热系数各理论模型的比较
Fig.3.23　Comparison of theoretical models of reinforced concrete thermal conductivity

图3.24给出了钢筋混凝土导热系数试验值与串-并联模型和并-串联模型等效导热系数的比较。可以看出，试验值基本落在了两模型围成的区域内，说明用串-并联和并-串联模型估算钢筋混凝土导热系数具有合理性。同时，竖向和水平向配筋的试验值接近区域的上界，即更接近并-串联模型的计算值，当钢筋体积分数为3.4%时，试验值超过了计算值，这说明当钢筋双向布置且体积分数较大时，钢筋的内热桥作用明显，这与3.3.2节结论相一致。另一方面，对于本试验试件来说，钢筋竖向和水平向布置且体积分数较大，影响了试件中混凝土粗骨料的均匀分布，也可能导致该情况导热系数增大。图3.25给出了试验值与上述四种理论模型的等效导热系数的对比。

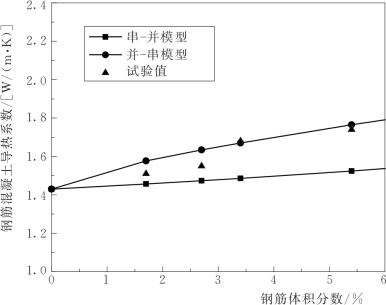
图3.24　钢筋混凝土导热系数试验值与串-并联和并-串联模型等效导热系数的比较
Fig.3.24　Comparison of test values and calculated equivalent thermal conductivity of series-parallel and parallel-series models

（3）钢筋横向配置时钢筋混凝土导热系数的理论分析。

钢筋横向贯通配置时，钢筋混凝土试件形态符合并联模型。在计量区域内，钢筋的体积分数v1=A1/A=379.94/10000=3.8%，混凝土的体积分数v2=A2/A=1-v1=96.2%。由并联模型计算公式（3.8）可知，

图3.25　RCCW11和RCCW12试件正面图（单位：mm）
Fig.3.25　Front view of specimen RCCW11 and RCCW12

试验值为2.0790W/（m·K），比计算值小16%，说明试验过程中，在钢筋截面积范围内有一定量的热量没有直接通过钢筋传递到冷侧，而是通过钢筋传到混凝土后再传到冷侧。这与3.3.3节的结论相佐证。

钢筋横向未贯通配置时，在计量区域内钢筋混凝土试件形态符合串-并联模型或并-串联模型。在串-并联模型中，先考虑串联，

再考虑并联模型，

在并-串联模型中，先考虑并联模型，

再考虑串联模型，

试验值为1.97W/（m·K），未介于两模型计算值范围内，且比上界大了8.8%。说明串-并联模型和并-串联模型对于钢筋横向集中布置情况缺乏适用性，但采用并-串联模型可近似预测实际值。