大多数工程材料都是由多种材料复合而成的,混凝土是最为常见的复合材料之一。复合材料的导热系数与各组分的导热系数、各组分在混合物中的形状、排列、含量及取向等因素有关[20,21]。如果复合材料各组分截面间存在界面热阻,也将影响其导热系数[21,22]。与混凝土相比,水泥砂浆和粗骨料导热系数的离散性较小。因此,在细观尺度上,混凝土可看作由连续相水泥砂浆和分散相粗骨料组成的两相复合材料。在复合材料等效导热系数理论模型基础上,混凝土导热系数的预测模型主要有如下几种。
(1)不考虑界面热阻的串联模型和并联模型。
热量在材料中传递时会受到阻力,即热阻。当热量在材料内部以热传导的方式传递时,遇到的热阻称为导热热阻。导热热阻定义为
![]()
式中:R为导热热阻,(m2·K)/W;L为热流通道长度,m;A为热流通道面积,m2;λ为材料导热系数,W/(m·K)。
如果将热阻看做电阻,借鉴串并联电路的电阻计算方法,可以计算复合材料的等效热阻以及等效导热系数[21]。
图3.3和图3.4给出了两相复合材料体系的串联模型和并联模型及相应的等效热阻网络图。设组分1和组分2的导热系数分别为λ1和λ2,体积分数分别为v1和v2,热流通道长度分别为L1和L2,热流通道面积分别为A1和A2。
串联体系中两组分的热流通道面积相同(A1=A2=A),因此,v1=L1/L,v2=L2/L。利用式(3.6),借鉴串联体系电路总电阻的计算方法,可以得到两相复合材料串联模型的等效导热系数为:

并联体系中两组分的热流通道长度相同(L1=L2=L),因此,v1=A1/A,v2=A2/A。利用式(3.6),借鉴并联体系电路总电阻的计算方法,可以得到两相复合材料并联模型的等效导热系数为:
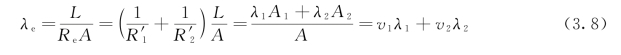
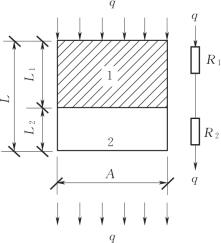
图3.3 串联模型
Fig.3.3 Series model

图3.4 并联模型
Fig.3.4 Parallel model
串联模型适用于计算不存在界面热阻的层状结构复合材料垂直于交界面方向的等效导热系数,并联模型适用于计算层状结构复合材料平行于交界面方向的等效导热系数。实际上,复合材料组分之间界面的方向往往是随机分布的,在不存在界面热阻的情况下,用串联模型和并联模型算出来的等效导热系数对应于两相复合材料实际导热系数的下界和上界。因此,串联模型和并联模型可以用于估算复合材料等效导热系数的大致范围。
(2)不考虑界面热阻的Maxwell模型及其推广模型。
Maxwell模型是较早的导热模型[21,23]。两相复合材料的分散相粒子在连续相基体中均匀分布,各粒子之间没有相互影响,利用远场方法(far-field methodology)可以推导出不考虑界面热阻的复合材料等效导热系数λe的Maxwell公式为:

式中:λ1和λ2分别为连续相基体和分散相粒子的导热系数;V2为分散相粒子的体积百分数。
Maxwell模型适用于分散相含量较低和两相导热系数相差较小的情况,试验数据与理论曲线非常一致。当分散相含量较高时,试验数据与理论曲线有相当大的差异。出现这种差异的原因是,当分散相含量较高时,粒子之间不再是孤立的,相互之间的影响也就不容忽视。此外,当连续相和分散相的导热系数的差别较大时,分散相粒子的形状对复合材料的导热系数将会产生较大的影响[24]。
Harmathy将混凝土作为两相体,其中水泥浆体为连续相,考虑孔隙率及含湿量影响确定等效固体导热系数(λpt),集料的体积分数为VA、导热系数为λA,得到混凝土导热系数计算公式[25,26]

Bruggeman通过分步增加分散相粒子的方法,来考虑分散相含量增加到很高时,粒子之间的相互影响,推导出不考虑界面热阻的复合材料等效导热系数λe的Maxwell方程微分形式[27]

通过积分变换,得到考虑分散相粒子相互影响的等效导热系数隐式方程计算公式
![]()
Hamilton-Crosser提出了考虑分散相粒子形状的复合材料等效导热系数计算公式[21,28]:
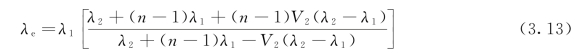
式中:n=3/ψ,ψ为粒子的球形度。当n=3时,式(3.13)即为Maxwell模型计算式(3.9);当n=1时,为串联模型计算式(3.7);当n趋向于无穷大时,为并联模型计算式(3.8)。
(3)考虑界面热阻的Maxwell模型及其推广模型。
不考虑界面热阻时,如果分散相导热系数λ2高于连续相基体导热系数λ1,则复合材料等效导热系数λe高于λ1,且随着分散相导热系数及其体积分数的增加而增加。但研究发现,有时加入小粒径高导热粒子后,复合材料等效导热系数没有像预期的那样明显提高甚至降低[21],根本原因是基体与粒子间存在界面热阻。分散相粒径越小,在相同体积含量下,其表面积越大,界面热阻越显著。当界面热阻效应超过分散相导热系数的贡献时,就会出现导热系数降低的现象。(https://www.xing528.com)
Hasselman和Johnson基于Maxwell模型且考虑界面热阻的影响,沿用Maxwell公式的方法,推导出考虑界面热阻的Maxwell模型的两相复合材料等效导热系数计算公式[29]
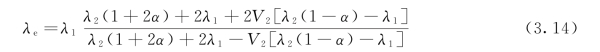
式中:α=γBdλ1/r2,r2为球形粒子的半径;γBd为单位界面热阻,其定义为
![]()
式中:qBd为界面热流密度,ΔT为界面温差。
如果界面热阻不存在,即α=0,式(3.14)即还原为Maxwell模型计算式(3.9)。
Every和Tzou等借鉴Bruggeman公式的微分法,推导出考虑界面热阻时的高粒子含量复合材料等效导热系数计算公式,如式(3.16)所示[21,30]。当α=0时,式(3.16)即还原为Bruggeman公式(3.12)。
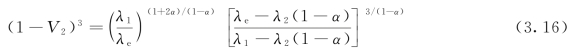
(4)Campbell-Allen模型。
Campbell-Allen和Thorne假定混凝土是由连续的砂浆组成,集料是分散分布在砂浆中,热传导在混凝土内部沿两条平行的路径:一条通过连接的砂浆层,一条通过由骨料和砂浆组成的层。同时假定集料在混凝土中的几何排列是有规律的,给出混凝土导热系数的理论公式为

式中:M=1-(1-p)1/3,p为砂浆在混凝土中的体积含量,λ为导热系数,其下标m和a分别代表砂浆和集料。
(5)Kook-Han Kim模型。
Kook-Han Kim通过试验回归,建立了混凝土导热系数与混凝土中骨料的体积含量、水灰比、温度、含水率以及砂率之间的关系[15,31]

式中:λc为混凝土的导热系数,vg为混凝土中骨料的体积含量,W/C为水灰比,T为温度,Rh为含水率,ρs为砂率;λref为当vg=0.70、W/C=0.4、T=20℃、Rh=1.0时混凝土导热系数值,取2.37W/(m·K)。
(6)朱伯芳模型。
朱伯芳院士认为在初步设计阶段尚未取得混凝土热性能的试验值时,可利用表3.1,根据混凝土各组成成分的重量百分比进行估算,并建议估算值乘以1.05的修正系数,其表达式如下
![]()
式中:λp、λw、λs、λg分别为水泥、水、细骨料、粗骨料的导热系数;ωp、ωw、ωs、ωg分别为水泥、水、细骨料、粗骨料的质量占混凝土总质量的百分比。
表3.1 估算混凝土导热系数的原材料导热系数
Table 3.1 Thermal conductivity of raw materials used for estimating that of concrete
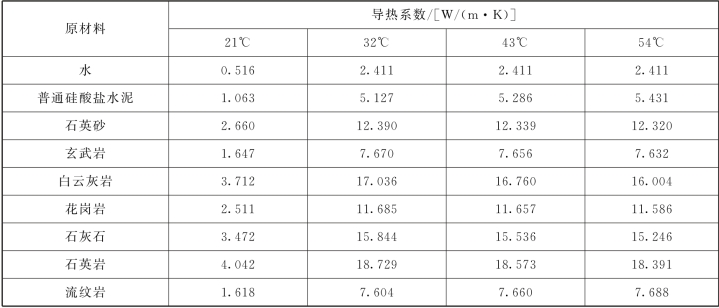
Khan通过试验研究分析表明[11],Harmathy计算式(3.10)计算值超出试验值17%~49%。随着粗骨料导热系数的增大,Campbell-Allen和Thorne的计算式(3.17)计算值超出试验值13%~32%;饱和状态时,在-13%~8%之间浮动。因此,式(3.17)较式(3.10)更适用于计算混凝土的导热系数。
张伟平等依据文献[11]的试验结果对混凝土导热系数预测模型进行了分析[21]。结果表明:在饱和状态下,混凝土实测导热系数基本位于串联模型和并联模型计算值之间,随着实测值的增大(骨料导热系数增大),串、并联模型的差异呈增大的趋势;Maxwell模型和Bruggeman模型计算值与实测值吻合得较好,相对误差在-13%~17%之间;说明在饱和状态下,由于粗骨料和水泥砂浆界面处存在水,导致界面热阻不显著。在干燥状态下,混凝土等效导热系数计算值,包括串联模型计算值几乎都大于实测值;这主要与干燥状态下粗骨料与水泥砂浆之间存在显著的界面热阻,导致导热系数降低有关。利用考虑界面热阻的Hasselman-Johnson计算式(3.14),求得试验条件下界面热阻系数α在0.114~0.289之间,均值为0.205。粗骨料形状、含量、级配不同,粗骨料的表面积即粗骨料与水泥砂浆的界面不同,界面热阻将不同。无论是饱和状态还是干燥状态下,Maxwell模型和Bruggeman模型的计算值相差均不大,说明在试验条件下(粗骨料体积分数为47%),相邻骨料之间的相互影响不显著。
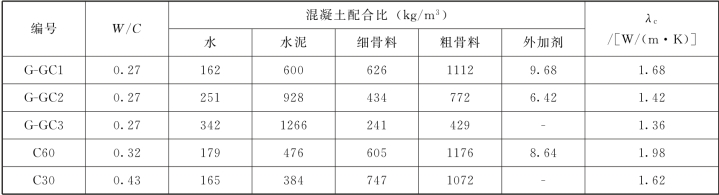
张枫等采用防护热板法进行了混凝土导热系数测试[31]。试验混凝土原材料采用复合硅酸盐水泥和S90级磨细高性能混凝土矿渣复合掺和料、中砂、玄武岩碎石、萘系早强高效减水剂和自来水,配合比和导热系数测试结果见表3.2。采用Hamilton-Crosser模型计算式(3.13)、Campbell-Allen模型计算式(3.17)、Kook-Han Kim模型计算式(3.18)和朱伯芳模型计算式(3.19)对试验结果进行预测,结果表明:混凝土导热系数计算值与试验值的误差随着混凝土导热系数的增加而减小。其中Campbell-Allen模型的计算值比试验值高15%~23%,Hamilton-Crosser模型的计算值比试验值高3%~28%,朱伯芳模型的计算值比试验值高0~27%,Kook-Han Kim模型的计算值与试验值符合的最好。
表3.2 混凝土配合比与导热系数试验结果
Table 3.2 Mix proportion and test results of thermal conductivity of concrete
本章结合钢筋混凝土内置保温层组合剪力墙的保温性能,进行了如下试验研究工作[32-38]:
1)对钢筋混凝土内置保温层组合剪力墙的原级配混凝土、细石混凝土、二次混合混凝土试件,进行了导热系数试验,分析了石子体积率、砂率、石浆比等因素对混凝土导热系数的影响,并进行显著性分析。
2)对竖向配筋混凝土、竖向和水平向配筋混凝土、横向配筋混凝土试件的导热系数进行试验,分析了钢筋布置方向、钢筋体积分数对钢筋混凝土导热系数的影响规律。
3)根据上述试验结果,基于已有材料导热系数预测模型,建立了考虑石浆比和钢筋体积分数的混凝土导热系数预测模型。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




