堤坝地基渗透稳定可靠性及加固方案分析

由于历史的原因，服役堤防和土石坝工程都不同程度地存在地基渗透稳定性问题，对服役工程的加固处理和提高防洪标准是当前及今后防洪工程建设的重要任务之一。在堤坝一类的水工建筑物中的渗透稳定性问题，其表现的主要形式包括管涌、流土及接触冲刷或接触流土等［3，289］。在理论上，目前对有关渗透破坏的失效机理研究还没有很成熟的结论，确定性的计算和校核方法也是在具体工程试验基础上进行的［221，289］；另外，由于服役防洪工程在运行期间（或汛期的抢险期间），可能使用不同材料及以不同形式进行加固（或抢险）、或加厚某部位、或在下游出渗点的排水和盖重的材料与形式不同，增加了服役堤坝工程的渗透稳定可靠性分析的难度。

在理论上，对土石坝和堤防的地基渗透稳定的可靠性分析，一般是按照土体的渗流理论计算通过土坡的水力渗透坡降，再将其与土体的临界坡降一起组成广义极限状态方程，然后分析该极限状态方程中的随机变量及其产生的综合变量的随机特性，得出该极限状态方程下的可靠度（或渗透破坏的风险率）。对于无反滤保护层时的坝体（堤防）与地基的渗透出逸点，设其水力坡降J为广义荷载效应，而土体的临界水力坡降［J］为广义承载力，定义当J＞［J］为破坏状态，则坝体或坝基的渗透变形破坏的风险率（或失效概率）为式（8.62）的形式［221］。要表达式（8.62）的概率密度函数f（J）是很困难的，因为其不仅与土体本身的性质和渗流边界条件有关，还与上下游水位差等随机因素有关，所以一些文献将计算公式离散化处理［221］，这样的计算是将洪水的过程模拟与渗透变形破坏结合的理论方法。对于给定的洪水位，如果f（J）能够统计得出，则直接对公式积分可得出失效概率计算，一般采用MC法，但是，f（J）很难统计得出，所以这种理论方法较难实现。

为避免理论上计算的复杂性，下面根据现行的设计规范［292，296］和工程结构可靠性理论的基本原理，对常见的在下游设排水盖重层结构形式的堤坝工程，给出其地基渗透可靠性的计算模型，并通过一个例题说明其在实际工程加固设计中的应用。

8.7.3.1　基于设计规范的地基渗透稳定的极限状态分析

按照现行的设计规范［292，296］，对没有反滤保护层的堤防及土石坝工程的地基渗透变形稳定的要求是，坝基的渗透出逸点的比降应小于材料的允许渗透比降；如果坝基的表层土的渗透系数小于下层土的渗透系数，而下游渗透出逸点的比降满足规范中的公式（即比降较大）时，则应该设置排水盖重层或排水减压井。根据工程结构可靠性的基本原理和上述的渗透稳定要求，可将材料的允许渗透比降认定为广义承载力［221］。这种方法定义的广义承载力，其形式简单，但是其中隐含的基本变量很多，包括土体材料的颗粒直径大小、级配及结构、孔隙率和容重等，还与施工的质量有关，一般是对服役坝体的土体进行实验后得出其随机数字特征。如果收集有土体渗透临界坡降分布范围资料，可直接将其设为广义承载力R＝［J］，［J］即是土体的临界渗透水力坡降。这种方法可用于任何坝型，尤其是均质土坝或堤防。

斜墙式土石坝无反滤保护层，但有压重时，其抵抗渗流变形破坏的广义承载力和荷载效应分析如下。如图8.9为土石坝（或堤防）概化模型。假定斜墙具有很好的防渗性能（不透水），土体的渗透破坏多表现为通过透水层的砂土地基的集中渗流对土体的冲刷（即管涌破坏）。

图8.9　堤防和斜墙式土石坝断面的概化示意图（有双层地基和下游覆盖）

在汛期高水位长期作用下，粘性土层的薄弱处有可能被承压水顶穿，形成集中出水口。由力学平衡条件，发生管涌时的渗透水的剩余水头（广义荷载效应）为γwhap，而此时的抵抗渗透破坏广义承载力可以写为［296］：

式中：hap为双层坝（堤）基表层弱透水层底板下界面处的剩余水头，可由下式简化计算［292，296］：

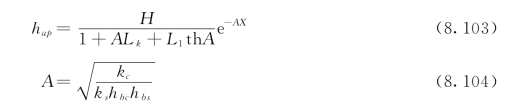
式（8.102）～式（8.104）中：A为越流系数；γw为水的容重；γnk为粘土的浮容重；dks为坝（堤）下水渠（塘）下粘土层的有效厚度；γsb为压盖土体（岩土）的容重；tsb为透水压盖的厚度；H为洪水位的高度；Lk为有效渗径的长度；L1为坝前铺盖宽度；hbc为不透水坝基粘土层厚度；hbs为透水坝基砂土层厚度；kc为粘土的渗透系数；ks为砂土的渗透系数（上述参数见图8.9）。

由于天然或人为因素，致使表层粘性土厚薄不均产生抗渗强度大小不等，在坝（堤）后背水侧往往有土坑形成的水塘、低洼地（见图8.9）。因此，坝（堤）后水渠（塘）下粘土层的有效厚度dks为随机变量，X为距离堤角C点的坐标（有效长度），可按照确定值计算。此时，堤坝的地基渗透稳定的极限状态方程为：

这种方法确定的广义承载力，表示的是在出逸点的有效抵抗受到上下游水位差产生的水力坡降的能力，计算比较容易实现。极限状态方程中的基本变量较多，需要进一步分析基本变量的随机特性，可由误差传递公式分析其中综合变量R和S的统计参数，建立定量预测堤防渗流风险率的实用模型［297］。

8.7.3.2　服役堤坝地基渗透稳定的可靠性分析

渗透变形失效模式下按风险率理论计算的方法较为复杂，如果考虑的是区间洪水位时更是如此，要求构造和分析在不同的水位下的渗透水力坡降的概率密度函数f（J），并分析其统计参数。而上述基于设计规范的服役土石坝（堤防）结构的渗透稳定可靠性分析方法，其组成的极限状态及其方程在形式上则较为简单［298］。尽管其中的变量多，但是其中的多数变量之间是相互独立的，因为有些是结构尺寸变量、另外一些是材料的物理参数变量（如渗透性能等），其综合随机变量（广义抗力R和荷载效应S）的统计参数比较容易分析。

（1）堤坝地基渗透稳定可靠性分析中的综合变量随机特性。土石坝及堤防工程的地基渗透稳定可靠性，其广义极限状态方程在形式上概括为Z＝R－S，该方程的形式是简单的，但其中的综合变量R和S的统计参数及随机特性的分析是关键。

(www.xing528.com)

如果变量随机的特性已知，则按上述方法计算渗透稳定可靠指标是可行的。如果模拟随机变量及其概率模型，可使用MC法等。对于不同的堤坝的上下游水位差ΔH，可根据不同洪水的水位随机性等，分析在不同洪水位时的渗透破坏概率，为设防标准下的渗透稳定加固决策服务。

8.7.3.3　堤坝地基渗透稳定加固方案分析

由于服役堤坝的有关尺寸及材料参数的随机性（分布及统计参数等），可根据实测值进行统计分析后（有的参数可作为确定值）参加计算，所以通过上述的分析方法可进行服役堤坝的地基渗透稳定可靠性分析，还可为不满足渗透稳定要求的堤坝地基的加固设计提供依据，给出较为经济的方案。下面分析一个算例，并选择经济的加固方案。

【例8.7】服役土石坝的剖面如图8.9所示，下游无反滤保护层也无水，其上、下游坡率（正态分布）均值分别为3.00、3.50，变异系数为0.01；现有坝顶高程（正态分布）均值为31.00m，变异系数为0.02。其他作为常量的参数是，粘土的浮容重γnk为9.00kN/m3，压盖土体的容重γsb为18.00kN/m3；坝基粘土层厚度hbc为5.50m，坝顶宽度B为7.00m；坝基砂土层厚度hbs为3.50m，粘土的天然容重γ为19.60kN/m3。其他的有关变量参数和概率分布见表8.14，计算坝前洪水水位（洪水频率为0.2%时的校核水位）均值为hw＝29.50m、变异系数为0.05时的地基渗透稳定可靠度，并为加固设计提出方案。

表8.14　服役土石坝的尺寸与材料变量的参数及概率分布

经过分析，并考虑到综合变量抗力R与荷载效应S的概率分布类型对计算结论影响很小，为简化计算，设两个综合变量都为正态分布。通过计算，坝前铺盖宽度对地基渗透变形稳定可靠指标的影响不大，当其宽度从0.00m增加到25.00m，可靠指标从2.686增加到3.081，增加的比例是14.69%，计算的结果见表8.15。可以定性地分析，如果坝高越高，则增加的铺盖宽度对其下游渗透变形的可靠性影响越有限，因为大部分渗透水头由坝底宽度形成的渗径消杀。

表8.15　坝前铺盖宽度L1对渗透变形可靠指标的影响

而压盖宽度对渗透变形稳定可靠指标的影响较大，计算的结果见表8.16；增加坝后的透水压盖宽度，其下游防止渗透变形的可靠性将迅速增加，效果很明显，当压盖宽度从0.00m增加到50.00m，可靠指标从2.211增加到4.390，增加的比例是98.55%。

表8.16　坝后透水压盖宽度X对渗透变形可靠指标的影响

另外，下游透水压盖厚度和粘土层有效厚度对渗透变形稳定可靠指标的影响，其分析的结论见表8.17。结论表明，坝下游的透水压盖厚度的增加，对提高其下游防止渗透变形的可靠性有较为显著的作用。当透水压盖厚度从2.50m增加到5.50m，可靠指标（β1）从1.886增加到了3.314，增加的比例是75.72%；而坝后粘土层有效厚度对可靠性的影响最为显著，其有效厚度从2.50m增加到5.50m，可靠指标（β2）从0.174提高到了3.081，增加的比例是非常大的（相应的失效概率从43.09%降为0.35%）。因此，对中小型土石坝工程或堤防工程来说，增加坝后粘土层有效厚度是渗透变形不满足要求时加固的最重要的措施。为有效地防止下游出现渗透变形失效，在条件允许的情况下，应该首先考虑的是垂直防渗措施，以便快速提高其渗透稳定可靠性。

表8.17　下游透水压盖厚度和坝后粘土层有效厚度对渗透变形稳定可靠指标的影响

上述计算结论见图8.10，在本算例中，增加坝后粘土层有效厚度时的可靠指标增加更快。

图8.10　下游透水压盖厚度dks和坝后粘土层有效厚度tsb对渗透变形可靠指标的影响

分析计算的结论还表明，上、下游坡率对渗透变形稳定可靠指标的影响并不显著，减缓坝坡不是防止渗透破坏加固的最重要的措施。通过分析，每增加0.50的坡率，可靠指标提高的幅度大约为10%；但是，每增加0.50的坡率，在本例题中则每延米的坝长要增加333m3的土方量，即使仅仅是100m长的土坝，则将增加3万多m3的土方量，所以并不是很理想的加固方法。另外，压盖厚度的变异性、广义抗力概率分布形式等对渗透变形稳定可靠指标的影响都不显著。当然，对不同型式、不同规模的土石坝工程来说，为有效地防止下游出现渗透变形失效和滑动稳定失效的具体措施应该是不同的。