8.6.2.1 现有堤防工程的条件失效概率定性分析
根据实际工程经验判断,可以比较容易地得出堤防工程系统的条件失效概率Pf(H)的两个极端值,即:
(1)洪水位H处于与堤防基础相同高程时,Pf(H)=0.00;
(2)洪水位H处于或接近于堤防顶部高程时,Pf(H)=1.00。
由于PS=1-Pf,上述两个极端的条件失效概率对应的可靠度则分别为PS=1.00和PS=0.00。
当现有堤防工程出现在上述两个极端洪水位值之间的洪水位时,其可靠度的变化规律则与堤防的工程质量、堤防结构的几何尺寸、土体的抗剪强度与渗透性能、基础的构造与排水设施的有效性等有关。根据有关研究成果与工程经验判断,现有堤防的可靠度函数PS(H)与条件失效概率函数Pf(H)与洪水位之间有5种可能的模型,如图8.4所示。(https://www.xing528.com)
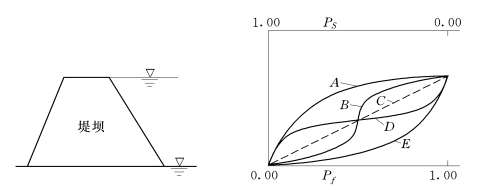
图8.4 服役堤防工程可能的可靠度与洪水位函数模型
在图8.4中,曲线A是“模型化的质量良好”的现有堤防的条件失效概率(和可靠度)函数模型,曲线形状表现为在低水位时低失效概率而有较高的可靠度,直到洪水位相当高时才使得失效概率增大;曲线R则是“模型化的质量差”的现有堤防的条件失效概率(和可靠度)函数模型,曲线形状是在低洪水位时就出现了可靠度的较大降低;曲线B是实际上的质量较好的一种堤防的失效条件概率(和可靠度)函数模型,洪水位较低时类似于曲线R,即低洪水位时可靠度降低较多,而高洪水位时表现为可靠度降低不多;曲线D为另一种实际上的质量较差的堤防条件失效概率(和可靠度)函数模型,曲线表现形式与曲线B相反,即在低水位时偏于质量较好的堤防可靠度曲线A,而在高水位时偏于质量较差的堤防可靠度曲线R。曲线C是一种假设简化的线性模型,即堤防条件失效概率(和可靠度)和洪水位的函数关系为线性。
上述的现有堤防工程条件失效概率(或可靠度)和洪水位定性的函数关系,可用于基于可靠性的费用效益模式,以对堤防加高加固的设防标准进行决策。由于历史的原因,除城市市区附近的河段外,我国的堤防大多是土堤,而且土堤是由历史遗留下来,并历代加高培厚形成的,大多数堤防工程的质量较差。结合我国的现有堤防工程的这一实际情况,在对现有堤防进行可靠性评估和加固决策时,建议用质量较差的堤防条件失效概率(和可靠度)函数模型,即曲线D,以策安全。至于曲线C,由于是线性关系,比较简单。当洪水位到达堤防顶高程时,其失效概率也并不一定为1.00,故这种模型是偏安全的。
8.6.2.2 现有堤防工程系统可靠度计算

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




