8.5.1.1 维修加固效益模式
在不维修加固的前提下,随着结构的服役期延长,其可靠性必然下降。因此,为维持结构一定水平的可靠性,必须及时采取必要的维修和加固。但是,维修加固是有前提条件的,首先是结构是否还有利用价值,其次是从经济角度出发,旧结构的维修加固之后的产出应大于维修费用[24]:
![]()
式中:U为结构维修加固后在后续服役期中经济效益的期望值;ΔU为U的增加部分;C为结构失效损失的期望值;ΔC为维修加固后C的减少部分;Cr为维修加固费用。
式(8.40)是一个基于投入产出的维修加固效益分析模式,其中涉及的因素比较复杂。该式的特点是使结构分析与经济分析结合起来,但其中要解决的问题还有以下几个。
(1)C及ΔC的计算。C包括结构失效带来的直接损失和间接损失,而ΔC一般用维修加固后所增加的可靠度ΔPS与C之积表示,即CΔPS。ΔPS的计算涉及到后续使用基准期T'(或加固后剩余使用寿命)、结构允许失效概率[PS]等。
(2)U及ΔU的计算。U的计算常用每年带给结构维修加固投资者的经济效益与加固后剩余使用年限乘积表示,而ΔU=UΔPS。同样,ΔU与T'及[PS](允许的失效概率)有关,而T'确定涉及因素众多。
(3)由于银行采用复利发放投资贷款,Cr的计算与维修时间及利率有关,因此,Cr是一个动态指标(与时间有关)。维修时间越后延,考虑银行贷款利率的影响时,则Cr可能越小;但越延后维修,投入的费用越大,增加部分则可能抵消了利率所减少部分。
(4)是采用一次维修加固,使维修后的结构失效概率大幅减少,还是采用多次维修,每次增加一部分可靠度ΔPSi的方案;每次维修到什么程度(即要求在现有基础上再增加多大的可靠度ΔPSi)等都需要决策分析。(https://www.xing528.com)
从上述分析可知,服役结构的维修加固的决策与效益分析涉及到结构计算理论、结构可靠性理论及经济分析等众多学科。式(8.40)的投资效益模式是基于经济学一般原理提出的,涉及到具体的结构维修加固,则比较复杂。
8.5.1.2 基于可靠度的服役结构维修加固决策模型
(1)可靠性决策模型。以结构评估后必须加固为例,即按T'计算(无论T'多大)的PS低于按现行的设计标准要求的[PS],一次性维修与多次维修加固的可靠性变化(即动态可靠性)如图8.3所示。
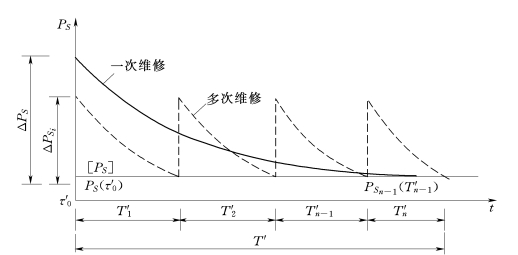
图8.3 一次与多次维修加固的动态可靠性



免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




