构件计算可靠指标与安全等级划分关系

8.1.2.1　RC 结构构件的可靠指标计算

现行的鉴定标准是根据n＝R/γ0S的值来评定混凝土结构构件承载能力等级的［188］，其对应的等级是au级等四级。现取n＝R/γ0S为1.10，1.00，0.95，0.90和0.85，其中，γ0为结构重要性系数；分别计算其对应的可靠指标β值。如果在获得混凝土构件的承载力衰减规律，并考虑抗力衰减和继续服役基准期的影响基础上，计算出的β值与设计标准［36］中要求的［β］值相比较，就可以根据计算指标按照鉴定标准的等级划分构件的安全等级，即根据检测资料直接得到现有RC结构构件的安全等级。

对于按混凝土结构设计规范［36］设计的结构构件，应该满足Rk/γR＝γ0（γGGk＋γQQk），其中，γG，γQ和γR分别为永久荷载、可变荷载和抗力的分项系数；Gk，Qk和Rk分别为永久荷载、可变荷载和抗力的标准值。

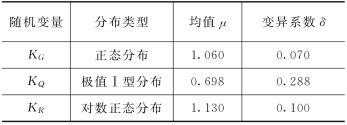
按设计规范［36］，构件的可靠指标与可变荷载和永久荷载的标准值的比值有关。对于一般的结构，γ0，γG，γQ和γR可分别取1.0，1.2，1.4和1.1，则有Rk＝1.1（1.2Gk＋1.4Qk）。令ρ＝Qk/Gk，在建筑结构中，ρ通常取为0.10，0.25，0.50，1.00和2.00。永久荷载效应G，可变荷载效应Q和抗力R均为随机变量，分别表示为G＝KGGk，Q＝KQQk和R＝KRRk。其中，KG、KQ、KR也都是随机变量，其分布类型和统计参数可参考有关规范取得［35］。对于RC构件，这3个随机变量的分布类型和参数见表8.1。

表8.1　民用建筑结构RC构件的G，Q和抗力R分布及其统计参数

按上述参数，可用JC法分别计算不同的结构或构件重要性系数，分项系数和n及不同的ρ值时的可靠指标β值。

8.1.2.2　不同的后续服役基准期，并考虑抗力衰减的构件β值计算

对于可变荷载效应，其标准值的取值与设计（或继续服役）的基准期有关，并按荷载组合采用结构设计（或继续服役）基准期的最大值。因此，现有结构或构件的可变荷载的标准值的取得，必须引入相应的调整系数［42，107，220］。对以50年为设计基准期时的现有建筑结构构件，其继续服役基准期的荷载标准值的调整系数可根据“等荷载超越概率原则”来确定［42，211，220］，该原则基于的假设是“继续服役基准期内的荷载超越水平与设计基准期内的相同”。(www.xing528.com)

设后续服役基准期为T＇，建筑结构在T＇内的楼面活荷载标准值的调整系数为λ＝QkT＇/Qk，QkT＇为T＇内的可变荷载效应。根据结构构件的继续服役基准期和后续继续使用年限，按“等荷载超越概率原则”可得楼面的持久性和临时性活荷载标准值的调整系数，在此基础上得出可变荷载的组合后的标准值调整系数λ［42，107］。

实际上的构件抗力是衰减的，与不同的继续使用年限有关。抗力随时间的增长不断降低，抗力和活荷载效应本质上均为随机过程，在后续服役基准期T＇内构件的失效概率可表示为［93，232］：

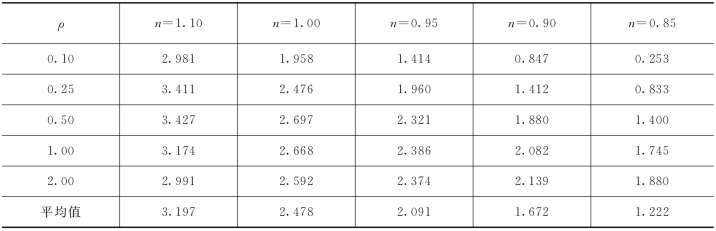
表8.2　后续使用30年的办公楼RC构件的计算可靠指标

当然，在大气环境下的一般腐蚀情况下，如果存在现有构件的实测材料性能变化值或实验值，则可分析得到现有RC构件的抗力衰减规律和不同的继续使用年限下的抗力统计数字特性，并用统计方法得到不同使用年限后的锈蚀RC构件抗力的计算模式不确定性等［282］，更准确地预测后续服役期内的可靠指标。

分别计算t为10年、20年、40年和50年时考虑抗力衰减的情况（此时可能包括设计的使用时间，如鉴定时已经使用了30年，后续再使用20年，则在原来的设计使用年限之内，共使用50年；但如果使用了30年，再拟继续使用30年，则超过的原设计使用的50年，共使用60年），仍然用上述抗力衰减规律和可变荷载的调整系数及组合，当ρ＝0.5时的计算结论见表8.3。

表8.3的结论变化规律见图8.1，其中，t＝0年时是按规范设计而不考虑抗力衰减时构件的可靠指标［35］。