6.2.2.1 可靠性界限及统计特性
到目前为止，对结构动力可靠性界限的研究还不充分，即使是对随机性界限（界限为随机变量）的研究。在考虑结构抗力瞬变性时，随机界限是时间t（t∈［0，Te］）的函数，但确切的界限λ的数字特征应满足的条件研究得不充分［10，26］。可靠性界限反映了结构在抵抗动荷载作用时的能力，实际上也是结构抗力的反映。为此，可考虑用类似于结构抗力的时变模型的形式，构建可靠性界限的随机过程的模型。
如前所述，在不修复的前提下，结构抗力有3个时变统计特征，即抗力均值函数为单调下降的，方差函数为单调增加，抗力的自相关系数是时段起点与时段长度的单调降函数。分析结构的动力可靠性界限性质，由于考虑结构在动荷载作用下的损伤及积累，因而也有类似的特点。因此，可靠性随机过程界限是非平稳和非齐次的随机过程。随机过程的模拟方法一般有谐波合成法和线性滤波器法［22，260］。但对于λ（t）来说，只有上述定性的结论，没有定量的实测数据作为模拟的依据，这两种方法都难实现。下面由类似于结构抗力的时变模型的形式，模拟可靠性界限的随机过程。
设结构的可靠性随机过程界限为{λ（t），t∈［0，Te］}，其中Te为动荷载持续时间，其均值和方差函数为R［λ（t）］、D［λ（t）］，自相关系数为ρ［λ（t），λ（t＋Δt）］。为简便起见，可设λ的均值函数R［λ（t）］及方差函数D［λ（t）］为指数函数形式：
表6.1 条件可靠度PS（t）
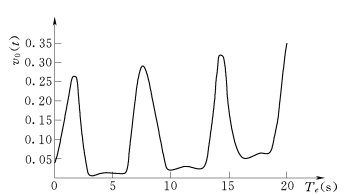
图6.2 期望穿阈率v0（t）随时间的变化图
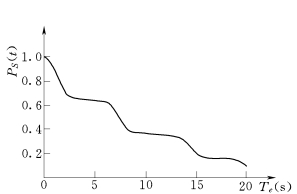
图6.3 可靠性函数PS（t）曲线
(www.xing528.com)
表6.2 条件可靠度PS（t）
6.2.2.2 确定性衰减函数时的可靠性随机过程界限
6.2.2.3 随机性衰减函数时的可靠性随机过程界限
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
