动态可靠性验证服役结构的条件-5.2.2

若考虑抗力R的时变性，则上述“旧有结构比新结构的可靠性高”的结论是不成立的，因为随着t与L的增加，抗力R必然下降。确定性RP条件下的服役结构可靠性研究较多，下面讨论的是考虑结构的抗力时变性的验证荷载（随机变量）条件下服役结构动态可靠性［232］。

按现行规范［9，35］，设结构的永久荷载效应为G（与时间无关的随机变量），可变荷载效应为Q（t），结构抗力随机过程为R（t）。结构已使用N年，再服役M年内的结构可靠性问题可用验证荷载下的条件概率求得。将N年和M年分成等时段，时段数分别为n和m，即τn＝N/n，τm＝M/m。Q（t）与R（t）离散为n和m个随机变量Q（ti）和R（ti），如图5.3所示，τn与τm可以相同或不同。

考虑当前时刻τ＇0之前结构未失效，有：

将G＋QN（t）作为验证荷载，再考虑到R（t）的相关性，当前时刻τ＇0处的抗力统计数字特性按第3章的随机性验证荷载作用下抗力数字特征计算公式从i＝1开始（即第1段）推求。若G、QN（t）与R（t）相互独立，则第i＋1段（i≤n＋1）的抗力R的后验密度函数为：

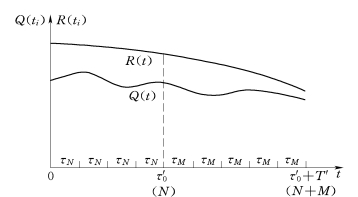
图5.3　验证荷载下的抗力与可变荷载等时段的离散

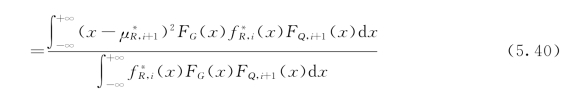
求出的R（t）在τ＇0处（分段推求）的均值与方差，即为在验证荷载G＋QN（t）作用后的R（t）的后验分布数字特征，也即为对设计抗力的修正值。若已知抗力随机过程离散后的随机变量分布类型，则可分析后续服役期M年内的可靠度。

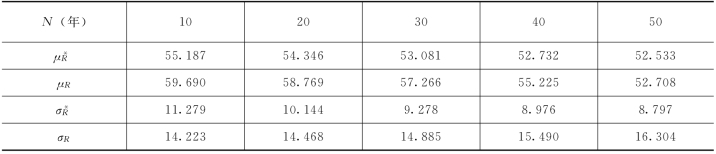
【例5.2】继续［例5.1］。如果设计的抗力均值和方差函数为E［R（t）］＝60exp（－5.183×10－5t2）（kN·m），D［R（t）］＝200exp（1.138×10－4t2）（kN·m）2。已使用N年（N＝10，20，…，50），求继续服役M年的可靠性。当前时刻τ＇0处的抗力未检测，由上述方法验证求得，其他参数（包括荷载参数及分布）同［例5.1］。此梁在建成初期（t＝0）抗力（随机变量）均值为60kN·m、方差为200（kN·m）2。利用式（5.37）～式（5.40）数值积分得使用N年后抗力R（t）在各时刻数字特征，列于表5.4（单位kN·m，表中μR与σR为设计值）。考虑使用N年后所受到的验证荷载（包括恒载、持久性和临时性活载），在同一时刻抗力的均方差比设计值小（方差小更多），均值也比设计值小。抗力的概率密度曲线中低强度部分被验证荷载“过滤”［174］，从而提高了结构构件的计算可靠度。

表5.4　使用N年后的R（t）各时刻随机变量的数字特征　单位：kN·m

(www.xing528.com)

（1）按设计抗力并考虑其衰减的结构动态可靠性。首先计算设计抗力及设计功能函数的相关系数，按第3章的独立增量过程计算的设计抗力相关系数ρ［R（t），R（t＋Δt）］＝exp［－5.689×10－5（2t＋Δt）Δt］；再由式（5.10）计算设计功能函数的平均相关系数Zj），列于表5.5中。

表5.5　设计状态下的功能函数相关系数

用JC法按β（ti）＝φ－1{PS［R（ti）－G－Q（t）＞0］}计算β（ti），再利用上述串联系统计算的近似算法求得后续服役期内的可靠度和相应的可靠指标，如图5.4和图5.5所示。

（2）已使用N＝20年后的动态可靠性。若该梁已使用20年，则继续服役期内的抗力考虑已使用期的验证荷载，抗力的均值和方差分别为E［R（t）］＝60exp（－5.183×10－5t2）－4.423和D［R（t）］＝200exp（1.138×10－4t2）－106.422（t≥20年），用表5.4的N＝20年的值为依据修正设计抗力的均值与方差函数，分别得到在未来30年中各时段的均值和方差。R（t）的相关性按独立增量过程分析，同样求得后30年功能函数的相关系数。用JC法按β（ti）计算β（ti），再利用按串联系统计算的近似算法求得后续服役期内的可靠度和相应的可靠指标，如图5.4和图5.5所示。

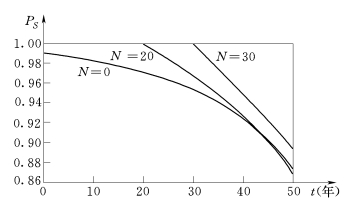
图5.4　服役结构的动态可靠度

（3）已使用N＝30年后的动态可靠度。若已使用30年，类似地得到抗力均值与方差函数（t≥30年），R（t）的相关系数仍然由独立增量过程求得。同样用JC法按β（ti）求其可靠指标，再利用按串联系统计算的近似算法求得后续服役期内的可靠度和相应的可靠指标，如图5.4和图5.5所示。

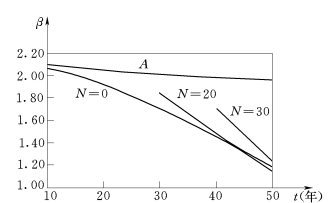
图5.5　服役结构动态可靠指标

从图5.4中可以看出，考虑了验证荷载之后的结构可靠度得以提高，而且N＝20年和N＝30年两条曲线，随着继续使用基准期的延长是趋近一致的，但N＝30年时比N＝20年可靠度提高的比例更大。图5.5是上述结果相应的可靠指标β的趋势图，其中A线为不考虑抗力随时间变化，即当时的β（活荷载采用持久性活荷载的任意时点分布值与临时活荷载在设计基准期内的最大值组合），为时不变可靠指标，此时β值变化很小（其下降是由于荷载效应随基准期的增加引起的）。

以上的结构动态可靠度分析方法中R（t）为随机过程，而且可考虑当前时刻τ＇0的抗力实测值对后续服役期抗力的影响。如果视R（t）为随机变量，用衰减函数φ（t）来描述t时刻（t＞τ＇0）的抗力，而且验证荷载效应为确定值xP，则问题变得十分简单［233］。