

式中:R(ti)为服役构件任一时刻ti的抗力;Q(ti)为其任一时刻ti的可变荷载效应。
将服役构件继续服役的目标基准期T'等分成n个时段,时段长为τ=T'/n,可变荷载效应随机过程Q(t)和抗力随机过程R(t)离散为n个随机变量Q(ti)和R(ti),如图5.1所示。其中,R(ti)可以取第i个τ中的抗力平均值或取为ti=(i-0.5)τ的抗力值;Q(ti)为τ内的荷载效应最大值。
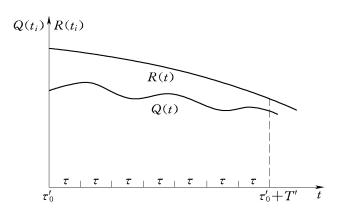
图5.1 抗力与可变荷载效应的等时段离散
由此,式(5.4)改写为:

上式相当于等时段τ的mT'个串联系统的可靠度问题。由于R(ti)(i=1,2,…,mT')是相关的,上式计算比较困难。若设Q(ti)相互独立,此时式(5.5)可变为[86]:

式中:FQτ(·)是Q(ti)的概率密度函数;fG(g)是G的概率密度函数;fR1,…,Rn(r1,…,rn)是R(t1),…,R(tn)的联合概率密度函数。
式(5.6)仍然是一个高维积分问题,且尚需知R(t1),…,R(tn)的联合分布概率密度函数,一般很难求解。为此,需要进行近似计算或变换。
5.1.1.1 按串联系统计算的近似算法


式(5.11)计算的可靠度是偏于保守(安全)的,计算方法也相对简单实用。
5.1.1.2 按串联系统计算的变量变换法(https://www.xing528.com)



表5.1 已服役20年梁的E[R(ti)]和σ[R(ti)] 单位:kN·m

按ti=(i-0.5)τ,并假定两个可变荷载效应之间相互独立,利用第3章的抗力独立增量过程的假设,计算的抗力相关系数见表5.2。
表5.2 服役梁各时段间的抗力相关系数ρ[R(ti),R(tj)]及ρ(Zi,Zj)


按JC法求解,此时验算点为:R*1=57.780N·m,R*2=39.500kN·m,R*3=34.500kN·m,G=32.020kN·m,Q*T'=3.500kN·m。
表5.3是两种算法的结果,①为按串联系统近似算法(数值积分)结果;②为变量变换法。两种算法结果较为相近,都是可行的,第①种电算较为简便,第②种方法既适合手算,也可电算。图5.2是该梁的时变失效概率变化图,随着T'的增大,失效概率迅速增大。

图5.2 服役梁的时变失效概率
①—近似算法;②—变量变换法
表5.3 服役梁的时变失效概率

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




