服役工程结构荷载概率模型及组合

4.2.1.1　永久荷载

永久荷载是在设计基准期内其值不随时间变化，或变化与平均值相比可以忽略不计的荷载。在拟建设计阶段，由于涉及诸多的不确定因素（如计算结构自重涉及的构件截面形状、几何尺寸等因素），永久荷载的概率模型一般以正态分布的随机变量来描述［35，187］。

服役结构的永久荷载模型的确定，依赖于对其信息的掌握以及对其未来情况的判断。对于服役结构，在已使用期永久荷载的自身信息较多，对继续使用期［τ＇0，τ＇0＋T＇］内的永久荷载可以根据使用情况量测后进行比较准确的预测。其中，对结构自重和设备自重等（设计时为随机变量），此时可按确定性永久荷载处理；如果考虑在实际量测时的误差，则仍可按照随机变量描述；若在未来使用期内，设计时的永久荷载只能确定其将在该时间段内保持一种随机状态时，也按随机性的永久荷载处理（如作用于结构上的土压力和水压力等）。4.2.1.2

可变荷载

可变荷载指在设计基准内，其值随时间变化且其变化与平均值比不可忽略。此类荷载的随机特性描述应为随机过程，目前建筑结构设计规范提出的模型是平稳二项随机过程，并模型化为等时段的矩形波过程（或等时段矩形波函数）［35，187］。除等时段的矩形波过程外，还有平稳高斯过程和泊松过程等［11，12］。但是，不同性质和不同的目标基准期的可变荷载，其随机概率模型及参数是不同的。

（1）等时段平稳二项过程。等时段的平稳二项过程，适用于描述变化较平缓的可变荷载，包括建筑结构楼面（及屋面）的持久性活荷载，或在结构空间中占有的持续时间较长的家具及设备荷载等。仍将该荷载样本函数模型化为等时段的矩形波函数，则服役结构的荷载概率模型为{Q（t），t∈［τ＇0，τ＇0＋T＇］}，T＇为服役结构继续服役的基准期，如图4.3所示。

该模型的假定仍然同设计规范［35］，只是其中的基准期为T＇，任意时点的概率分布函数FQ（x）的统计参数应通过实测调查取得［42］。

（2）等时段平稳矩形过程。若p＝1，则荷载在每个阶段是必然出现的，其他假定同等时段的平稳二项过程，荷载模型即成为等时段的平稳矩形波过程，即式（4.6），其适用于描述变化较频繁的可变荷载，如风荷载和雪荷载等。

4.2.1.3　偶然荷载

偶然荷载是设计基准期内不一定出现的荷载，而一旦出现，其量值很大且持续时间较短。在整个设计基准期内，荷载发生的现象为稀有事件，且它发生的概率与时间无关，可用泊松过程来描述荷载发生变化的时点过程。因此，偶然荷载（如地震和爆炸等）的随机过程，可以用泊松过程或跨阈理论描述。

（1）泊松过程。泊松过程适用于交差次数是独立的小概率事件发生次数的描述，适合于描述偶然荷载的随机性。设泊松过程{N（t），t≥0}，t以前荷载发生变化的次数N（t）服从泊松分布，则：

图4.3　等时段的平稳二项过程

图4.4　复合泊松点过程的离散脉冲函数

图4.5　平稳离散型过程的样本函数

4.2.1.4　几种荷载模型的分析(www.xing528.com)

等时段平稳二项过程比矩形波过程的分析复杂一些，但在荷载组合时，后者假定荷载

表4.1　跨阈率计算

由以上分析的结果，F（T＇，x）及FT＇（x）如图4.6所示。

图4.6　年最大风压和T′＝20年及T′＝30年最大风压的概率分布曲线

①—20年，极值分布理论；②—30年，极值分布理论；③—20年，跨阈理论；④—30年，跨阈理论

4.2.1.5　荷载效应组合规则和JCSS组合规则）［11］。现行的建筑结构设计规范采用的是经过修改的JCSS组合规则［35，187］。

服役工程结构可靠性分析中的荷载效应组合，其方法仍然可用上述的修改JCSS组合规则，即JCSS提出的一种近似的荷载组合概率模型，并结合工程经验判断来处理服役结构荷载的组合问题。这种方法的基本假定是可变荷载Qi（t）的样本函数为平稳二项过程，并与荷载效应S（t）保持线性关系。设有n种可变荷载参与组合，将模型化后的各荷载Qi（t）在基准期T＇内的总时段数ri，按顺序由小到大排列（即r1≤r2≤…≤rn），然后取任一个Qi（t）在［0，T＇］内的最大荷载效应maxSi（t）（t∈［τ＇0，τ＇0＋T＇］）与其他荷载效应进行组合，可得几种组合的最大荷载效应（综合荷载效应）Smj（j＝1，2，…，n），选择其最不利者作为荷载组合的最后结果，用于可靠度计算。

对属于复合泊松过程的瞬时脉冲荷载，由于上述组合的排序原则是：荷载等值持续作用于结构的时间越长（或时段数越少），其排位越低（或越高），即综合荷载效应Smj应排在越前面，因此，这种瞬时脉冲荷载在组合中只要求出其效应在T＇内及其他荷载时段内最大值分布，无需任意时点的分布。假设k个脉冲荷载相互独立，且两个及以上同时出现的概率忽略，则k个瞬时脉冲荷载的荷载效应最大值分布为［12］：

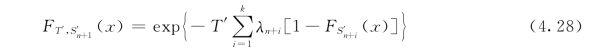
式中：λn＋i和FS＇n＋i（x）分别为第n＋i个（i＝1，2，…，k）荷载在单位时间内的平均出现次数和荷载效应任意时点的概率分布函数。

在与其他可变荷载组合时，将上式得出的综合荷载效应的概率分布函数FT＇，S＇n＋i（x）作为JCSS组合中的第n＋1个荷载（其总时段数最大）参与组合。

由于持久性可变荷载变化与临时性可变荷载出现的时间及荷载量值的变化都是随机性的，对于除楼面活荷载之外的其他可变荷载（如在维修施工中的临时性堆贮荷载等），直接将设计规范中的荷载量值引入会产生较大的误差，尤其对服役结构来说，若有使用历史上的荷载样本，则必须考虑已有荷载的信息，使荷载的统计参数与实际相符或接近。

另外，有的研究将持久性可变荷载视为泊松方波过程（其变化次数描述为泊松过程），临时性可变荷载视为滤过泊松方波过程（其变化次数也描述为泊松过程），给出过设计结构在设计基准期T内这两种可变荷载组合的概率分布函数的解析解。其数值计算例题表明，FT（x）在大于0.5的概率值之后的范围内能够较好地与蒙特卡洛方法近似［83］。服役结构的可变荷载组合若采用这种组合后的概率分布函数解析解，也可将持久性可变荷载在继续服役基准期T＇内划分为相等时段（每段长为ra），且每段ra内变化一次；临时性可变荷载在T＇内划分的相等时段为ra，则有持久性可变荷载和临时性可变荷载组合后的概率分布函数的解析解为：

式中：FT＇（x）为在继续服役基准期T＇内，两种可变荷载组合的概率分布函数；Fb（·）为任意时点临时性可变荷载的概率分布函数；fa（sa）为任意时点持久性可变荷载的密度函数；ra与rb分别为持久性可变荷载和临时性可变荷载年平均变化次数，raT＇相当于在T＇内持久性可变荷载的平均变化次数。

在形式上，式（4.29）与设计结构的上述两种可变荷载组合后的解析解相同。但是，服役结构可变荷载的任意时点概率分布函数及统计参数、荷载的持时长度等可根据调查和统计使用历史上的荷载样本获得，并可获得式（4.29）中的Fb（·）和fa（sa）的类型及统计参数等；再通过均值和标准差的定义和上式表示的分布函数FT＇（x），用数值积分的方法可计算出两种荷载组合后的统计参数。至于其分布类型，可经过假设检验得出。按现行设计规范［35，187］中的等时段模型（即将T划分为r＝raT个等时段）得出的楼面活荷载的组合分布，是上述解析解的近似解。

荷载效应组合规则和统计分析远比单个荷载效应问题复杂，迄今仍没有比较成熟合理的方法，其精确解的求得涉及较复杂的积分方程求解，目前的各种方法都存在不少值得研究的问题［58，99］。一般情况下，服役结构的荷载组合及其参数统计在方法上可借鉴设计拟建结构的荷载组合分析方法。