随机性验证荷载下的抗力估计|[书名]服役结构可靠性及应用

对随机性的验证荷载研究不多［62，64，206］，但实际的验证荷载是存在随机性的。设验证荷载效应是随机变量Q*，且Q*作用之后结构未受破坏，不考虑Q*作用后结构抗力的降低，Q*作用之前R的分布函数为FR（x）、密度函数为fR（x），根据条件概率，R的后验分布函数FR*（x）为：

其中：

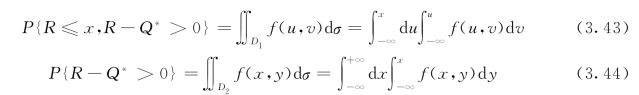
式中：f（x，y）为R与Q*的联合概率分布密度函数，D1和D2的积分区域如图3.5所示。

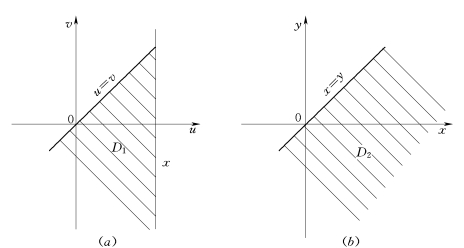
图3.5　联合概率分布f（x，y）的积分区域示意图

若R与Q*相互独立，则：

有：

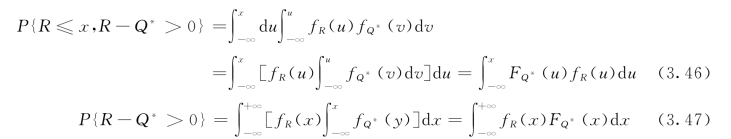
则式（3.42）变为：

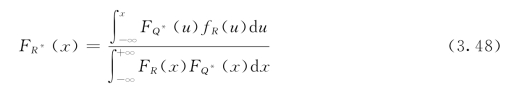
此时R的后验分布密度函数为：

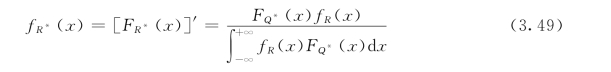
式中：FQ*（x）为Q*的分布函数。

3.3.2.1　R为正态分布

(www.xing528.com)

3.3.2.2　R为对数正态分布

表3.6　Q*对R的数字特征的影响（μR＝200，DR＝50）

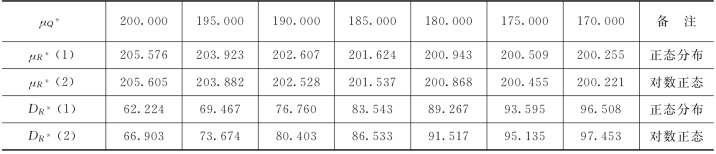
可以预计，Q*不同分布时R的均值及方差的变化趋势，与Q*为确定值（即RP）时相同；Q*不同分布时的R的均值变化趋势如图3.6所示。

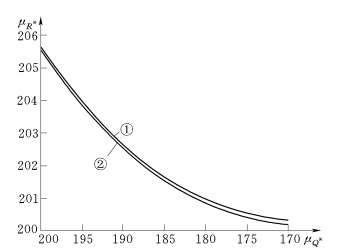
图3.6　R均值μR*随Q*均值μQ*的变化规律

①—R为正态分布；②—R为对数正态分布

Q*不同分布形式时的R的方差变化趋势如图3.7所示。另外，经过计算，若Q*的均值大于抗力设计均值μR时，经过验证荷载Q*后，结构抗力的均值与方差等数字特征的变化规律与［例3.3］相似。

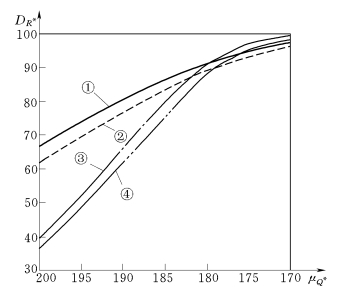
图3.7　R的方差DR*随验证荷载Q*的均值μQ*的变化规律

①—Q*为随机变量，R为对数正态分布；②—Q*为随机变量，R为正态分布；③—Q*为定值，R为对数正态分布；④—Q*为定值，R为正态分布（③与④为表3.4中的数值）

从计算的结果可得出如下结论：①验证荷载对抗力截尾的影响是明显的，无论R为何种分布，总的变化趋势是随着Q*的均值增大，影响越大；②Q*对对数正态分布R的方差影响比R是正态分布时大；③一般在Q*的均值为R的设计均值85%左右开始有影响；④随着Q*的变异系数的加大，对R的均值与方差影响减小，尤其是对方差的影响显著减小；⑤随Q*的变异系数增大，对R的变异系数影响也减小。因此，考虑验证荷载效应后，若不计其对抗力衰减的影响，对提高现有结构的计算可靠度将比较显著。

另外，若R与Q*相关，则随着其相关系数ρ的增大，抗力后验分布密度函数fR*（x）正偏程度加大，众值分布密度显著提高［180］。但一般地，R与Q*的相关性是比较小的。若R与Q*相关，如果两者均为正态分布，此时的R与Q*的联合概率分布密度函数为：

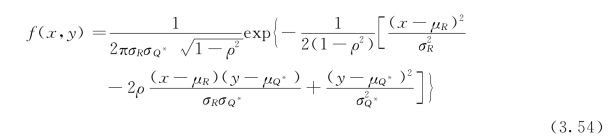
此时，代入式（3.42）～式（3.44）运算即可。但一般情况下，R与Q*的联合概率分布密度函数f（x，y）的分析很困难。

上述的讨论说明，随机性验证荷载的均值要达到设计抗力的均值85%左右才开始对后验分布抗力数字特征有影响；抗力的先验分布概率模型对抗力的后验分布数字特征影响不大，后验分布数字特征取决于随机性验证荷载的数字特征。