基本变量不确定性的描述处理方法

2.2.2.1　服役结构基本变量的不确定性来源

如在第1章中所述，服役结构的基本变量的不确定性产生于两个方面，一是在事件自然过程中，由于事件本身所固有的变异性、模糊性等造成的不确定性；另一种是由于估算或模拟带来的误差引起的（即系统误差），如由于模型的简化引起的误差，由于知识不完备引起的未确知性［12，23］。

服役结构在服役期前后的基本变量中，有些变量可能存在其中两种或三种不确定性（即同时具有随机性、模糊性和未确知性）。例如，结构设计时的构件强度有随机性，可以用统计方法来估计，但对具体构件，其强度有未确知性。另外，在结构的分析设计中，由于所考虑的阶段不同，可能存在不确定性的转移，其性质会有所变化。例如，在设计时，结构的抗力既有随机性，也有未确知性；而当前服役状态，应当只有未确知性与模糊性，不存在随机性（但如果考虑检测的误差，仍具有随机性），未来服役期内的抗力则明显具有随机性。未确知性又称弱不确定性，在有强不确定性（即模糊性与随机性）时，可以包括在强不确定性中进行处理［23］。

服役结构的可靠性分析是以自身信息为基础的，反映基本变量不确定性的是结构自身及其环境的信息。若能获得其建成之后的长期和完备的信息，无疑对其可靠性分析是相当有利的。但这样的信息收集不仅费时、费力，而且客观上也不太可能。对于大部分信息的采集，只能在一个较短时间内进行，以获得的小样本推断基本变量在未来的不确定性。

2.2.2.2　结构基本变量的不确定性描述处理方法概述

结构的随机不确定性是结构分析和设计中的一种主要不确定性，由于认识早，处理手段比较完善，以随机性为研究对象的结构随机可靠性理论已发展到实用阶段。随机不确定性的描述处理方法包括概率论、统计理论及随机过程理论等。信息的模糊性描述与处理，其数学工具是模糊数学。自1965年美国的扎德（Zadeh）创立模糊数学理论以来［164］，在结构可靠性理论方面得到一定的发展，同时形成了模糊聚类分析、模糊综合评判等评价方法，但离实用阶段尚有一定距离［25，57］。未确知性的描述处理，目前有两个主要学派，一是1976年美国的沙非（G.Shafer）提出的“信度理论”，其提出了在有限离散论域内的信度函数（Belief Function），主要以Dompster法则合成各种证据信息并形成信任函数［12，165］；另外一个是1978年模糊理论创建人Zadeh提出的从模糊集隶属函数中定义可能性测度的“可能度理论”［164］。除此之外，还有一些理论正待发展，如证据决策理论［166］，但这些研究尚未形成统一的理论体系。

（1）随机性的定量描述。对于基本变量的随机性，可根据有限的观测数据和适当的分布来近似描述。寻找这种描述方式，即确定随机变量的分布模型问题。一般地，可根据经验或理论估计先假定一种概率分布后，再按某种统计检验方法（拟合优良性检验）来肯定或者否定这种假定。若处理两个或两个以上变量时，还可以根据回归相关分析结论确定变量之间的关系。

在建筑工程结构可靠性分析中，荷载效应的随机概率分布一般情况下用永久荷载为正态分布模拟，而活荷载为极值Ⅰ型分布，但截面的抗力一般为对数正态分布［11，16，35］。现有的观测资料统计表明，建筑结构中的风、雪压年极值都不拒绝极值Ⅰ型分布［12］。不过，对于混凝土结构耐久性分析中的广义荷载，如混凝土碳化深度等，其分布模型的确定较困难，需根据实际情况进行假设检验［16，38］。

（2）未确知性的定量描述。基本变量的未确知性往往是在所谓的意识信息中表现的不确定性［12］。如调查的最高历史洪水位，由于调查对象主观上有随机性，一般不能用某一具体数值来全面描述，这种不确定性大多属于未确知性的。但是，被调查人员对不同的数值或其范围往往具有不同的信任程度，因此，可用信任函数或信任密度函数来反映其不确定性［12］，相当于用模糊性中的隶属度分布来描述。至于信任函数和信任密度函数的建立，目前一般的方法是用确定主观概率的概率盘法和区间分割法［12］。(www.xing528.com)

（3）模糊性的定量描述。描述事物的模糊性的数学工具是模糊数学，其核心是隶属函数的确定问题。有些信息由于某些原因，无法对其进行确定性描述，即只能认定其在一定程度上属于某一集合，从而产生隶属函数。设在给定论域U，U到［0，1］闭区间的任一映射：

来确定U的一个模糊子集即为的隶属函数，称为u对的隶属度［167］。

隶属函数的确定可以有模糊统计法，二元对比排序法和子集比较法等［25，57，167，168］，针对不同性质的问题可采用不同方法。隶属函数的确定，尽管有一定的主观性，但必须符合人们的共识，有相当程度的客观性，不可随意杜撰。

（4）基本变量不确定性的综合描述。对信息的不确定性，Lind曾用图2.2表示了上述三种不确定性及其相互关系［169］，指出处理它们有三种方法：当概念清晰而且数据众多时，用频度概率来描述这种不确定性，并用统计方法处理；当概念清晰而数据不足时，可以用主观概率来描述这种知识不完备的不确定性；上述两者之间的关系可以用Bayesian方法处理；对于概念不清晰的事物，则应用模糊集合来描述。除可进行模糊随机事件的概率分析外，对模糊性和随机性之间的关系，则认为尚无其他适当方法对这两类不确定性进行综合处理［169，170］。

这三类看来性质不同的不确定因素，归根到底，都来自知识不完备，都可以用概率密度表示，随机性用客观概率，其他两类用主观概率，而且都可以用Bayesian方法处理。模糊性和知识不完备性这两种不确定性用主观概率密度函数，其代表了当前专家的知识水平［170］。

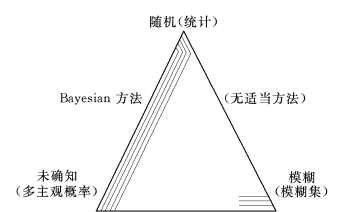
图2.2　不确定性及其处理［169］