驾驶节能，运行距离离散化及DP算法求解

1.单列车驾驶节能

单列车节能控制（Energy－efficient train control，EETC）问题，又称节能驾驶问题，是在考虑列车性能、线路条件的情况下，寻找一条满足时刻表给定区间运行时分约束的列车运行轨迹，以达到最小化列车运行能耗的目标。针对该问题的研究可以追溯至1960年代，以日本学者Ichikawa发表的文献为开端，之后在近几十年以来随着计算机、电子、控制与优化技术和理论的不断进步而发展更新，并逐渐将理论研究在实际系统中进行了应用。

EETC问题主要依据列车运行的牵引计算进行。该问题以列车运行的轨迹为优化对象，在数学上属于动态优化问题。随着最优控制理论与体系的发展，该问题通常被建模为最优控制问题进行分析与求解。对EETC问题的优化模型可以按照问题的寻优对象与离散化方式进行分类，具体分为两类：预设控制序列、寻找控制序列转换点和无预设控制序列；离散化距离（或时间）微元，寻找最优控制律。在该问题的场景建模过程中，通常考虑的要素包括：线路模型、列车模型、闭塞类型等。

针对EETC问题，在求解算法方面，采取的主流算法类型笔者将其分为四大类：解析法、规划算法、智能算法和其他算法。

1）解析法

最优控制问题的解析法基于苏联学者庞特里亚金等人在总结并运用古典变分法成果的基础上，提出的极小值（有时也称作极大值）原理（PMP）。该方法是控制向量约束时求解最优控制问题的有效工具，最初运用于连续系统，之后又推广于离散系统。

Ichikawa等建立了对于连续控制列车在水平坡度、不考虑限速条件下的节能运行速度曲线的数学模型，并采用PMP原理对其最优性条件进行了分析；Milroy针对连续控制的列车，以最小化运行过程中动力做功为目标，得出当区间长度较短、区间坡度很小时，列车运行工况包括最大牵引、惰行和最大制动三种；Asnis等基于PMP原理，证明了列车节能最优速度曲线包括最大牵引、巡航、惰行与最大制动四种工况；Khmelnitsky以时间和列车动能为状态变量、距离为自变量，考虑了变化的坡度和限速条件，对连续控制的列车的节能控制问题进行了研究，证明了当给定巡航控制模式速度，就可以唯一确定最优节能驾驶曲线，并据此提出了数值迭代算法进行列车运行轨迹的求解。

针对离散控制的内燃机列车，Howlett等考虑了变化的坡度，给出了能够确定节能最优控制策略的控制转换关键方程，并得到了由最优控制策略组成的最优运行轨迹；在上述基础上，Cheng等针对离散控制的内燃机车，同时考虑了变化的坡度和限速限制，在将区间划分为若干常数限速与常数坡度的子区间后，给出了相应最优控制转换的关键方程与求解方法，并证明了对于离散控制的列车，最优速度曲线可以由最大牵引、惰行、最大制动三种控制模式组成的锯齿状形式，以任意精度逼近连续控制列车的巡航模式。

进而，针对线路条件中存在陡峭坡度的情况下的EETC问题，SCG团队也进行了一系列的研究。

Howlett等指出，与不含陡峭坡度的列车节能运行最优控制序列不同，当列车处于陡峭的上坡区段时，由于列车即使采用全功率牵引也无法保持车速的匀速巡航（更无法使得车速加速上升），因此列车需要在进入陡峭的上坡区段之前提前实施最大牵引工况，并持续至列车离开陡峭坡度区段后，待车速恢复巡航速度止。在此过程中，列车速度将呈现先上升，在陡峭上坡范围内车速下降，之后离开陡峭上坡范围后车速重新上升的波动形式。同理，当列车处于陡峭的下坡区段时，由于重力分力的作用，列车此时虽采取惰行工况，车速仍然会加速上升，因此需要在列车进入陡峭的下坡区段之前提前实施惰行工况，并持续至列车离开陡峭坡度区段后，待车速恢复巡航速度止。在此过程中，列车速度将呈现先下降，在陡峭下坡范围内车速上升，之后离开陡峭坡度范围后车速重新下降的波动形式。之后Albrecht等在此基础上将仅在局部陡峭坡度的最优解完善至全局最优解，给出了包含陡峭坡度的变化坡度条件下的列车节能速度曲线一般模型与求解方法，并在文献中，运用摄动分析法给出了最优性与唯一性证明。

在实际工程应用方面，由于基于PMP的解析算法具有计算速度快的特点，SCG团队将上述研究成果开发了列车节能驾驶操纵指导系统，包括早期用于市内交通列车的Metromiser、用于长途货运列车的Cruismiser、Freightmiser以及近期的Energymiser系统。

2）规划算法

（1）动态规划（离散动态规划）算法

动态规划（Dynamic Programming，DP）算法是Richard E.Bellman于1957年提出的求解多级决策过程最优化的一种数学方法。国内外诸多学者通过将EETC问题离散化为多阶段决策问题，之后应用DP算法进行了求解。

Franke等考虑了变化的牵引能耗效率，将能耗效率建模为列车牵引力（制动力）和车速这两个因素的函数。并将列车站间运行距离进行离散化，作为离散的决策阶段，使用列车单位质量的动能和时间作为状态变量向量，并采用DP算法进行求解。Ko等采用非均匀网格的离散化方法：在列车发车与站间运行过程中采用较为稀疏的网格尺寸，在停站阶段采用较为精细的网格尺寸，改进了DP算法的数值计算精度。Vašak等针对EETC问题，将基本阻力方程采用分段线性仿射函数（PWA）的方法进行线性化处理，并采用DP算法进行求解。Miyatake等首先总结了在EETC问题中需要被考虑进列车运行轨迹优化的因素，包括牵引供电系统馈线损失、接触网电压与列车牵引力曲线之间的互相影响关系、列车制动过程中再生制动力与空气制动力之间的分配、列车运行阻力、线路坡度、车载或地面储能设施、牵引电机与逆变器的能量转化效率和信号系统；而后在考虑了储能装置、牵引供电馈线的能耗损失，以牵引变电所输出能耗为评价目标进行了EETC问题的研究，并使用DP算法进行了求解。Lu等针对EETC问题提出基于离散位置的列车节运轨迹搜索模型，并采用DP算法求解，并将DP算法结果与遗传算法、蚁群算法求解结果进行对比，得出DP算法的求解效果最好的结论。唐海川等以列车速度的改变量为控制变量，离散化列车区间运行距离为决策阶段进行建模，并采用了DP算法求解，并基于DP算法的回溯记录表特性，讨论了列车运行过程中的实时节能在线调整。Ghaviha等针对EETC问题，考虑了以列车牵引力（制动力）和速度为因素的变化的牵引能耗效率所导致的动态能耗转换损失，以离散化时间步长为决策阶段，速度与距离为状态量，速度的改变量为控制变量，进行了多阶段决策问题的建模求解，并采用了DP算法进行求解，设计了基于Android平台的驾驶辅助系统。Zhou等研究了高速铁路时刻表与列车运行轨迹的联合优化问题，采用拉格朗日松弛法对原问题进行解耦，在解耦后的单列车的节能轨迹优化子问题中，对高铁列车运行轨迹的优化采用了离散空间-时间-速度网络建模，并使用动态规划算法进行求解。Wang采用离散动态规划方法，分析讨论了在考虑列车长度因素时，将列车视为质量带模型的城轨列车EETC问题，并与采用单质点模型建模所得到的EETC问题的列车运行轨迹进行了对比。

（2）序列二次规划算法

序列二次规划（Sequential Quadratic Programming，SQP）算法是一种强有力的处理中、小规模非线性规划问题（NLP）的基于梯度的算法。SQP算法的主要思想是通过将原问题转化为一系列二次规划子问题，在每一迭代步通过求解一个二次规划子问题来确立一个下降方向，以减少价值函数来取得步长，并重复这些步骤直到逼近并求得原问题的最优解。这也是其成为二次规划算法的原因。SQP算法可以很好地处理非线性约束，而EETC问题又恰好包含诸多非线性条件与约束，因此国内外不少学者将其应用于该问题的研究中。

Miyatake应用SQP算法对EETC问题进行求解，指出SQP算法具有适合拓展应用至多维度控制变量输入的优点。Gu基于来自列车自动监督系统（Automatic Train Supervision，ATS）的实时调度信息，设计了一种针对城轨列车EETC问题的实时优化模型与算法：采用PMP原理，根据线路坡度、限速条件设定列车节能最优控制序列，并根据能量守恒原理以控制序列的转换点状态为决策变量，建立非线性规划模型，并采用SQP算法进行求解。在建模过程中，Gu认为城轨列车运行速度较低，因此可以根据旅行时间来确定列车平均速度下的基本阻力值，并将其代替变化的基本阻力值进行计算。

（3）混合整数线性规划算法

Wang等针对EETC问题，以列车运行能耗与舒适度的加权作为目标函数，通过采用分段仿射（Piece Wise Affine，PWA）方法将非线性列车模型转化为线性列车模型，同时对距离进行离散化处理，由此建立了EETC问题的混合整数线性规划模型，并采用现有的商业求解器（如CPLEX、Xpress－MP、GLPK等）进行求解。之后Wang等将EETC问题的混合整数线性规划（Mixed Integer Linear Programming，MILP）模型求解结果与伪谱法进行比较，得出伪谱法求解结果较好，但是MILP模型在计算时间消耗上优于伪谱法1至2个数量级的结论。之后Wang等又基于上述MILP模型，以列车运行的时间与单位质量动能为状态变量，考虑了固定闭塞与移动闭塞因素，对EETC问题进行了进一步的研究。相似的研究还有Wu等，考虑了在固定闭塞和列车延误的场景下，受到前行列车影响的后行列车EETC问题。Wu等采用PWA方法来线性化列车动力学模型，以离散距离建立了MILP模型优化两车运行轨迹，使得两车总能耗最小。

MILP方法除了在上述EETC问题中的应用之外，Lu还将MILP方法应用于求解部分轨迹优化问题中。所谓部分轨迹优化问题是相对于上述列车在站间全程运行的EETC问题而言的。上述EETC问题求解的是列车从上游车站至下游车站完整的运行轨迹，此时轨迹的初始点与末端点的列车速度均为零。而部分轨迹优化问题则是在列车运行过程中，列车从区间内任意位置xa运行至另一位置xb的轨迹。与EETC问题不同，该轨迹只包含区间部分范围，因此被称为部分轨迹优化问题。除此之外，部分轨迹优化问题的轨迹初始点与末端点的位置速度可以为设定的任意合法值，而不是EETC问题中起始端点速度均为零。

Lu等首先提出了部分轨迹优化问题，并假设该问题中不包含陡峭的坡度，且列车速度曲线随着距离是单调变化的，例如单调上升或者单调下降；并通过离散化距离的方式，建立了MILP模型，并采用商业优化求解器CPLEX进行了求解。之后Lu等考虑了为恒定值的列车牵引电机的运行效率，对MILP模型进行了改进，同时简化了线路坡度与限速条件，利用PMP原理进行了控制序列与切换规则的分析。Tan等基于上述研究，假设列车在无坡度的线路上运行，采用PMP原理进行了更深入的分析，移除了Lu等的研究中对于速度曲线随距离单调变化的假设，得到了更为完整的控制序列与切换规则；并建立了MILP模型进行求解，并将求解结果与伪谱法进行了对比。

（4）伪谱法

伪谱法是求解最优控制问题数值解的一种直接方法。伪谱法的思想是将连续的最优控制问题的状态与控制变量通过正交配点来进行离散化，并通过全局插值多项式逼近状态和控制变量，进而将最优控制问题转化为非线性规划问题进行求解。根据所采用的配点类型的不同，常见的用于求解最优控制问题的伪谱法包括但不限于Gauss伪谱法、Legendre伪谱法、Radau伪谱法、Chebyshev伪谱法等。EETC问题是一种典型的最优控制问题，国内外许多学者也将伪谱法应用于此问题的求解，并进行了深入的研究。

Wang等考虑了在固定闭塞信号条件下的EETC问题，分为两种情况：只能获得下一个闭塞分区信号信息、全程闭塞分区信号信息均为已知。考虑到EETC问题具有包含多阶段、非光滑的性质，Wang等将其建模为多阶段最优控制问题，并用包含Radau伪谱法的GPOPS求解器进行求解。Scheepmaker等同时考虑了列车与供电接触网效率，将EETC问题转化为多阶段最优控制问题，采用商业求解器GPOPS进行求解，并对比了不同效率对EETC问题求解结果的影响。Xiao等则是研究了有轨电车交通系统的EETC问题：考虑了交叉口信号灯约束、牵引供电接触网的无电区段等更加实际的工程因素约束条件，建立了多阶段最优控制模型，并使用包含自适应Legendre－Gauss－Radau伪谱法的商业求解器GPOPS－II进行求解。

3）智能算法

（1）启发式算法

启发式算法（Heuristic Algorithms，HA）是相对于最优算法被提出的，可以定义为一种基于直观或经验构造的算法，在可接受的花费（如计算时间、占用空间等）下给出待解决的优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度不一定可以事先预计。启发式算法是一种随机搜索算法，因此它搜索全局最优解的能力比较强；启发式算法不需要梯度，也不需要解析的目标函数，因此适用于处理那些没有解析目标函数和无法得到目标函数梯度信息的优化问题。同时，启发式算法还适用于解决同时有整数和连续变量的非线性混合优化问题。常见的启发式算法包括但不限于：遗传算法（Genetic Algorithm，GA）、蚁群算法（Ant Colony Optimization，ACO）、模拟退火算法（Simulated Annealing，SA）和粒子群优化算法（Particle Swarm Optimization，PSO）等。作为强有力的优化方法，国内外诸多学者对启发式算法在EETC问题上的应用进行了广泛且深入的研究。

遗传算法是一种被广泛应用于EETC问题求解的启发式算法。Chang等针对EETC问题设计了惰行控制方式，通过预先设置“惰行-牵引／制动……”控制序列，以控制序列的转换点为决策变量，建立优化模型，通过遗传算法进行求解。金炜东等讨论了列车在起伏坡道上的EETC问题，采用了构建局部优化仿真计算和全局寻优相配合的优化计算思想，即通过将线路划分为典型的子区间，根据节能原则给出优化的操纵序列形式，并使用仿真计算获得各个子区间列车能耗、运行时间与区间端点速度的数据，使用BP神经网络对各个子区间的数据关系进行拟合；再应用遗传算法对各个子区间的运行时间进行分配以实现全局优化求解。李玉生等针对EETC问题，在充分总结优秀司机的驾驶经验的基础上，提出了“坡道三分法”的机车手柄位变化原则，即在一段等坡度值的坡道上，司机变更手柄位的最大次数为2次，将坡道划分为三部分。并以手柄位具体值与手柄位变化位置作为决策变量，建立非线性优化问题，并采用遗传算法进行求解。付印平等针对EETC问题，通过将线路划分为包含起伏坡度的典型子区间，并预设子区间内的优化控制序列为“牵引、惰行、必要时动力制动、必要时空气制动、缓解”，以列车工况变化点的位置为决策变量，通过惩罚函数的方法建立无约束非线性优化问题，并采用遗传算法进行求解；并在此基础上，针对列车运行通过车站时可能会受到其他列车干扰的现象，采用变长度染色体遗传算法，结合工况序列表进行了建模与求解。丁勇等结合地铁列车的运行特点，提出了EETC问题的两阶段优化方法：阶段1，建立寻求站间最佳惰行控制次数和惰行控制点的优化模型；阶段2，建立各个站间区间运行时间的分配模型，并采用遗传算法进行求解。刘炜等提出变长实矩阵编码的多种群遗传算法对EETC问题进行求解，增强了算法的全局搜索能力。Huang等采用了多种群基因算法（Multi－population genetic algorithm）对单列车多区间的EETC问题进行了研究。邹临风等研究了EETC问题在列车辅助驾驶系统的应用：首先，分析了区间运行能耗与巡航速度之间的对应关系；其次，应用遗传算法分配各区间运行能耗，生成节能驾驶曲线。Liang等将是否超限速、停车精度、准点等多目标因素和惩罚函数方法融合于改进的遗传算法中进行EETC问题的求解。

在应用蚁群算法求解EETC问题方面，Ke针对固定闭塞和移动闭塞场景下的EETC问题，将区间划分为若干子区段，以各个子区段的平均速度为决策变量，建立了非线性优化模型，并设计了基于蚁群算法的长短蚂蚁算法（Max－min ant）对模型进行求解。Lu也应用了蚁群算法对EETC问题进行求解。Huang等采用两阶段方法，使用不同尺度的站间区间距离的离散化方式进行建模，并设计了改进蚁群算法进行求解。

在应用模拟退火算法求解EETC问题方面，陈万里提出了一种在不考虑坡度的条件下，通过离散化时间微元、动态罚函数的方法，将最优控制问题转化为无约束非线性规划问题，并使用模拟退火算法进行求解。刘炜等利用区间分割和迭代计算，通过离散化区间运行距离，以列车牵引力使用系数作为决策变量，将EETC问题转化为非线性规划问题进行求解。

在应用粒子群算法求解EETC问题方面，Domínguez等、Rodríguez等使用了多目标粒子群算法（Multi Objective Particale Swarm optimization，MOPSO）对地铁列车自动驾驶（Automatic Train Operation，ATO）系统的速度曲线设计过程建立了帕累托最优曲线，进行了节能、提高鲁棒性与准点的优化。贺德强等采用隔断分析的思想，通过离散化区间位置的方法，将列车站间运行过程分为若干阶段，并设计每个阶段包含预先设计控制序列或其中某些子序列，以矩阵向量编码，并采用粒子群寻优算法进行求解。黄友能等采用粒子群算法对单列车在多区间运行过程进行了两阶段优化：第1阶段优化列车站间运行轨迹，采用离散化距离的方法，优化各个离散距离内的列车目标速度；第2阶段在总运行时间不变的前提下分配各个区间的运行时间。Zhao等考虑了EETC问题中列车机械能与消耗的电能之间的耦合关系，采用了能够反映电气特性的更为精确的列车牵引系统模型进行了建模，并考虑了启动附加阻力的影响，通过对站间距离进行等距离散化的方式，应用粒子群算法优化离散距离的各个阶段的列车运行推荐速度。徐凯采用粒子群优化与布谷鸟搜索（Cuckoo Search，CS）相结合的方法，对城轨列车ATO曲线的设计过程进行仿真优化。他构建了多种群双层PSO－CS联合优化算法：在底层使用PSO算法对小种群进行寻优，高层使用CS算法进行深度优化。

（2）先进控制论方法

自20世纪70年代以来，随着计算机技术的广泛应用，自动控制技术有了很大的发展，先进控制论方法，又称先进过程控制（Advanced Process Control，APC）应运而生。先进控制理论内容丰富、涵盖面广，包括自适应控制、鲁棒控制、预测控制、模糊控制等。

1983年，Yasunobu设计了模糊控制器，首次将模糊控制应用于列车自动驾驶，并应用于车载ATO设备，在日本仙台地铁进行了现场试验。Carvajal－Carreño将模糊参数与NSGA－II优化算法相结合，对移动闭塞场景下的地铁列车车载ATO节能驾驶曲线进行优化设计。在此基础上，Carvajal－Carreño基于模糊控制设计了用于移动闭塞场景下的地铁列车速度曲线跟踪算法，从而减少了不必要的连续牵引制动的控制抖动周期，节约了列车运行能耗。Saadat采用模糊前瞻控制对柴油-电力混合动力机车进行了控制器设计，通过综合考虑列车电池状态（SoC）、前方线路坡度与目标速度等因素，控制列车手柄位，实现列车的节能控制。Bai综合考虑了控制的时效性与最优性之间的平衡，考虑机车运行过程中复杂时变的限速条件，设计了基于模糊规则的模型预测控制方法（Fuzzy Predictive Control，FPC），并开发了车载司机驾驶辅助系统，为司机节能驾驶提供操纵建议。

（3）基于学习的算法

Sekine针对列车自动驾驶提出双自由度模糊神经网络的控制系统，以吸收优秀司机的操纵经验规则。金炜东等讨论了列车在起伏坡道上的EETC问题，采用局部优化仿真计算和全局寻优相配合的优化计算思想，使用BP神经网络对各个子区间的数据关系进行拟合，再应用遗传算法对各个子区间的运行时间进行分配，以实现全局优化求解。余进设计了两级模糊神经网络，前一子网模拟优秀司机的操纵可获得在当前状态下应采取的最佳列车运行工况，后一子网根据列车当前状态与环境，得到列车在该工况及当前条件下的运行速度。Acikbas采用惰行控制的方法研究列车节能运行优化，模型采用人工神经网络（Artificial Neural Network，AN）拟合仿真软件中惰行点输入与运行时间、能耗输出之间的关系，再通过遗传算法进行全局优化。类似地，Chuang也采用ANN的方法通过仿真平台产生训练数据，对列车运行过程中惰行速度与运行时间、能耗之间的关系进行了拟合，以优化列车惰行控制进行节能。柏赟针对货物列车在停车制动阶段建立双层模糊神经网络模型：第一层子网通过样本训练计算基于制动初速度和制动距离的初始控制变量，第二层子网考虑加算坡道和牵引计算误差对制动距离的影响，以实现货物列车一次停车制动，有利于降低行车能耗。(www.xing528.com)

将深度学习与强化学习类方法应用于求解EETC问题上，Yin基于专家系统方法提出了地铁列车智能驾驶算法ITOE，并在此基础上与强化学习（Reinforcement Learning，RL）方法相结合，提出了列车智能驾驶算法ITOR，通过在线优化来减少列车运行能耗。之后，Yin融合了列车人工驾驶与列车自动驾驶各自的优点，提出了基于数据挖掘与数据融合的智能列车驾驶方法——STO（Semi－automatic Train Operation，半自动运行），采用分类和回归树（Classification And Regression Tree，CART）与集成学习方法，提取列车人工驾驶数据中的经验规则，并与列车自动驾驶数据进行融合，得到了STO方法，从而降低了列车运行能耗，提高了列车运行的舒适度。Liu采用自适应动态规划（Adaptive Dynamic Programming，ADP）方法对EETC问题进行了建模求解，并对比了在三种不同的价值函数下算法求解得到的列车运行轨迹。Cheng基于专家系统的方法，针对高铁列车运行场景建立了智能驾驶方法（Intelligent Driving Methods，IDMs）以提高列车自动驾驶的舒适度，降低运行能耗；同时，Cheng还考虑高铁运行场景下因线路长度长、速度快等特点造成的数据量巨大，难以直接应用于特征提取与学习的难点，提出了数据稀疏化的方法用于去除冗余数据，提高学习效率。Huang采用离散区间运行距离的模型，应用随机森林回归算法（Random Forest Regression Algorithm，RFR）和支持向量机回归（Support Vector Machine Regression，SVR）算法进行了基于数据驱动的列车节能运行最优速度轨迹曲线优化。

4）其他类算法

宿帅针对城轨列车EETC问题，基于PMP原理、列车运行能耗与运行时间的关系，提出分配能量微元的优化求解算法：以牵引力做功为目标函数进行最小化的优化，采用离散线路距离的方式，分配能量微元至各个细分区间进行搜索，从而获得最优轨迹，降低ATO运行过程中的能耗。之后，Su等应用上述算法在考虑了不同的车辆、线路环境等参数设置下，通过算法优化计算得到了列车节能驾驶最优速度曲线与区间运行能耗，分析了各个因素对于能耗的影响。接着，Su进一步考虑了牵引能耗传递效率这一特性，采用以列车车速和牵引力使用系数为自变量的变化的能耗效率，并基于能耗效率随牵引力使用效率单调递增这一特性，进行了EETC问题的研究。采用了基于PMP原理的分析方法，得出在考虑了上述特性的变化能耗效率时，列车节能最优运行过程将不包含“部分牵引力-匀速巡航”这一工况，该工况将由“最大牵引-惰行”这种控制序列对来代替，但是仍包含“部分制动力-匀速巡航”工况。并且基于上述结果，设计了基于离散运行距离，对子区间进行能量微元分配的数值算法，以计算列车节能运行轨迹。

Domínguez通过实地采集列车运行轨迹数据，建立了精确的列车运行模拟器。他考虑到由于固定闭塞系统，因此应答器提供的地-车单向通信传输的数据有限，故将列车ATO运行曲线采用“惰行速度、再牵引速度、巡航速度、制动减速度”这4个参数进行描述，并将上述参数按既定步长离散化，采用穷举的方法，建立运行时间与能耗之间的帕累托最优曲线关系。类似地，Zhao基于多列车模拟器，采用增强的暴力搜索算法（Enhanced Brute Force，EBF）进行列车节能驾驶轨迹的搜索。

2.多列车驾驶节能

上述单列车的节能控制问题是基于列车运行过程的牵引计算，聚焦于对单辆列车在站间区间运行过程中的控制或操纵方法的优化，减小列车机械能的消耗，以达到节能的目标。对于实际运营的城轨线路而言，同时在线运营的列车数目较多，列车在站间区间运行时存在频繁的牵引、制动工况。目前，城轨列车大多均已装备再生制动能量回收装置，因此存在以基于再生制动能量利用的角度，进行系统级的节能优化的方法。国内外诸多学者针对提高再生制动能量利用率以实现城轨列车节能运行方面进行了广泛而深入的研究。

1）节能运行图（含一体化优化方法）

节能运行图（EETT）是一种从运营角度降低城轨列车运行系统能耗的方法。EETT方法常见的思路是：①通过优化调整列车的站间运行时间、到站与发车时刻，协调同一供电分区内列车的再生制动与牵引工况，提高再生制动利用率以实现节能；②采用列车运行速度曲线与运行图一体化的优化方式，首先通过列车节能运行曲线，获得站间运行时分与最优能耗之间的帕累托曲线，再以诸如总旅行时间等为约束，根据客流特征、列车、线路特性等因素，进行各个站间区间运行时间的分配，以减少全程运行能耗。

在调整列车区间运行时间、到站与发车时刻的研究方面，Gordon首先提出了通过多列车协调控制来最大化再生制动能耗利用。Wong基于事件的交通流模型，通过对停站时间与站间运行时间的调整，以实现提高服务水平和降低运行能耗的目标，并设计了动态规划算法进行求解。Ramos首次提出了用牵引工况和制动工况的重叠时间作为衡量再生制动能量利用的指标，并建立了通过最大化同一供电分区内重叠时间的混合整数规划（Mixed Integer Programming，MIP）模型，并采用Cplex软件进行求解，以实现再生制动能量的最大化利用，节约系统能耗。Nasri以最大化再生制动能量的利用为目标，建立了地铁牵引系统的电气模型和列车运行图优化的整数规划模型，并使用遗传算法进行求解，分析了发车间隔和冗余时间对再生制动能量利用的影响。类似地，Peña－Alcaraz建立了地铁牵引供电系统的能量流模型，以估计能耗节约因数，并以最大化再生能量利用率为目标建立列车运行图优化模型，采用商业求解器SBB和Cplex进行求解。

Yang考虑了再生制动能量在相邻列车之间传递的场景，以最大化列车牵引与制动工况重叠时间为目标函数，以列车发车间隔、车站到发车时刻为决策变量，建立了整数规划模型，并设计了遗传算法进行求解。针对在线运行的列车存在不同载客量、各列牵引制动车性能差异等影响运行图能耗的因素，Yang考虑了不确定的列车质量以及变化的列车牵引力、制动力和基本阻力因素，以最小化列车牵引能耗为目标函数，建立了包含列车质量为随机变量的随机优化模型，并设计了基于仿真的遗传算法来求解，以进行节能运行图设计。之后，Yang综合考虑了系统能耗与乘客等待时间（服务水平），建立了双目标整数规划模型（TIP），并设计了遗传算法进行求解。在此基础上，Yang考虑了列车停站时间的不确定因素，以列车运行的净能量（牵引能耗减去再生制动能耗）和旅行时间最小为目标，建立了双目标优化模型，并采用ε－constraint和遗传算法进行求解，获得帕累托最优解。Liu等、刘宏杰等以最大化再生制动能量的利用为目标函数，并首次考虑了日运营列车车次数量和首末班车时间约束，建立了节能时刻表的优化模型，并首次采用了人工蜂群算法（Artificial Bee Colony，ABC）进行求解，获得了优于遗传算法的数值结果。

在利用一体化思想对城轨列车速度曲线与运行图进行一体化优化的研究方面，Su针对城轨列车运行曲线与运行图一体化的优化问题，在假设线路无坡度，城轨列车牵引力、制动力与基本阻力均为恒定值的前提下，建立了求解给定站间运行时间的列车节能运行曲线的解析算法，获得了列车区间运行时分与最优运行能耗的帕累托曲线关系，并在此基础上设计了数值算法，进行列车在各个站间区间的运行时间分配，使得列车运行的总牵引能耗最小，并应用上述结论设计了列车节能运行图。Su考虑了更加符合实际的列车模型，即随速度变化的牵引力和制动力与列车基本阻力，以及线路坡度因素，建立了一体化节能优化模型，模型以站间运行时间、列车周转时间、在线列车数量、列车间隔、列车运行曲线的牵引力与制动力使用率为决策变量，以最小化研究的时间范围内的所有列车牵引力做功为目标函数，并设计了用于求解上述一体化模型的IEE数值算法。更进一步，Su在考虑了再生制动因素的场景下，研究了城轨列车速度曲线与运行图的一体化优化问题。

Chen根据城轨区间长度将其分为短区间和长区间，并定义列车在短区间运行的控制序列为1次牵引策略，即“最大牵引-惰行-最大制动”控制序列；列车在长区间运行过程采用2次牵引策略，即“最大牵引-惰行-最大牵引-惰行-最大制动”控制序列。以列车发车时刻、工况序列转换点、到站时刻为决策变量，建立优化模型，采用粒子群优化算法进行速度曲线与时刻表的一体化优化求解。

Zhao考虑了传输损耗的因素，进行了城轨列车速度曲线与全日运行图的一体化研究，其中列车速度曲线的控制序列为“最大牵引-巡航-惰行-最大制动”的经典四阶段控制序列。Tian通过建立城轨系统直流牵引电路模型，以蒙特·卡罗仿真的方式，回归获得列车牵引能耗与再生制动能耗效率的系数，并以此为基础进行列车速度曲线的选择和运行图的一体化优化。

Zhou考虑了城市轨道交通场景下，含有陡峭坡度的线路条件时，列车运行曲线与运行图一体化节能优化问题，即将一体化优化问题解耦合为EETC问题与EETT问题。在EETC问题层面：假设线路均为恒定限速，并定义列车在包含陡峭下坡的最优控制序列为“最大牵引-［巡航-惰行］n-最大制动”，其中“［巡航-惰行］n”表示n对“巡航-惰行”控制序列，这使得列车充分利用陡峭下坡延长惰行范围。Zhou还指出，当n=1时，即为EETC问题经典的四阶段控制序列。他采用暴力搜索算法对EETC问题进行了求解。在EETT问题层面：以最小化列车运行的净能耗（牵引力做功减去再生制动能耗）为目标函数建立了优化模型，并采用一种改进的包含邻域搜索的遗传模拟退火算法（NS－GSA）进行求解。

步兵针对上述一体化问题，提出了多车协作节能控制的方法：他在假设只考虑2～3节列车，不考虑线路坡度，且只有一个供电分区的条件下，以时隙能量格模型进行净能耗的评估，通过预先生成的多组运行时间不同的节能驾驶轨迹曲线，供时刻表优化过程选择。除此之外，Feng采用大灾变遗传算法也对一体化问题进行了研究。

2）多列车协调节能控制

上述的节能运行图优化方法，或基于运行图与列车运行曲线调整的一体化优化方法，均需要对列车运行时刻表进行调整。而列车运行图的制定需要考虑诸多与运营相关的因素与约束（如运能匹配、协调换乘、首末班车等），从节能角度进行运行图的制定将受到诸多制约。因此，在满足运行图约束下，研究以系统能耗最优为目标的多列车协调节能控制（EETCoC）就应运而生。与单列车的EETC问题不同，EETCoC问题以系统最优为目标，此时列车在区间运行的过程中为了提升再生制动能量的使用，可能存在二次牵引加速或提前制动减速的操纵序列，这将使得EETCoC列车的控制序列与经典的EETC问题中四阶段（最大牵引-匀速巡航-惰行-最大制动）或三阶段（最大牵引-惰行-最大制动）的最优控制序列不同。国内外学者对此问题进行了一些研究。

Sun针对城轨列车运行过程中，相同供电分区内存在富余的再生制动能量未被吸收的场景，提出了一种多列车协同的思想，用以调整列车运行的部分速度曲线，以吸收多余的再生制动能量。Sun以再生制动多余能量产生的时间范围内，最大化列车依靠吸收富余能量运行的距离为目标函数，建立最优控制优化模型以进行列车的速度曲线调整。速度曲线协同调整距离范围内的平均速度相同为调整前后的平衡条件，将原轨迹中“巡航”或“牵引加速”的控制序列替换为“惰行-牵引加速-惰行”组成的控制策略。Sun研究并分析了更为一般的情况，并考虑了列车之间再生制动能量传递过程中的损失，建立了非线性目标函数与线性约束的优化模型，并用增广拉格朗日方法进行求解。Sun指出多余的再生制动能量应该优先分配给同方向、邻近的列车调整速度曲线使用。

唐海川考虑了同一供电分区内存在两列追踪运行的城轨列车的场景，建立了包含直流牵引变电所、列车、接触网与回流钢轨的电路拓扑模型，通过求解列车在不同牵引与制动功率下的电路方程，得到牵引变电所输出电压与电流。唐海川在假设前行列车运行轨迹已知的条件下，以两车运行的时间范围内，最小化牵引变电所输出的电能做功为目标函数，建立列车速度曲线节能优化模型，并通过对站间距离进行离散化，通过二次规划算法，求解后行追踪列车在各个离散微元的牵引力或制动力，从而获得最优追踪运行轨迹，降低系统运行能耗。Tang考虑了同一供电分区内存在两列上下行对向运行的城轨列车的场景，建立了包含直流牵引变电所、上下行列车、上下行接触网与回流钢轨的电路拓扑模型。类似地，通过求解列车在不同牵引与制动功率下的电路方程，得到牵引变电所输出电压与电流。Tang以两车运行的时间范围内，最小化牵引变电所输出的电能做功为目标函数，建立列车速度曲线节能优化模型。通过对站间距离进行离散化，使用遗传算法与适应度函数内添加晚点与运行距离偏离惩罚的惩罚函数方法，同时求解两列车在各个离散距离微元内的牵引力或制动力，从而获得最优轨迹。

Liu考虑了在同一供电分区、同一车站内追踪运行的两列地铁列车的协调控制的场景：前车按照EETC问题中最优控制序列的四阶段运行，即“最大牵引-匀速巡航-惰行-最大制动”，后车则采用三种不同的控制序列，分为：①与前车相同的四阶段控制序列；②五阶段控制序列，即“最大牵引-匀速巡航-最大牵引-惰行-制动”；③五阶段控制序列，即“最大牵引-惰行-最大牵引-惰行-制动”。Liu在不考虑陡峭坡度和线路限速的情况下，以最小化两列车运行机械能之和为目标函数，以工况转换点为决策变量，建立了优化模型，并采用启发式算法进行求解。Liu将上述两列车追踪运行场景扩展到三列车的运行过程中，他认为在同一个供电分区内至多包含三辆列车，因此可以将三辆列车视为一个小系统组群。他分析与讨论了在第1列车与第3列车不同的发车间隔条件下，第3列车的最优控制序列。以最小化三辆列车的牵引力与再生制动力做功的机械能代数和为目标函数，并采用启发式算法对各列车控制序列的转换点进行求解。

Bai考虑了同方向、多区间运行的地铁列车场景：预先设定确定的列车控制序列为“牵引-巡航-惰行-制动”四阶段，与EETC问题不同，在多列车协调控制环境下，为了提高再生制动的重合时间，列车的牵引与制动过程并非采用最大比率输出。Bai以最小化各个供电分区内列车的牵引力做功和制动力做功的代数和为目标函数，设定各辆列车的归一化的牵引力使用率、制动力使用率、巡航工况起点位置和惰行工况点位置为决策变量，建立基于固定控制序列寻找工况转换点的优化模型，并采用遗传算法与模拟退火算法组成的协同进化算法进行求解，并得出在提高再生制动能量使用率的多列车协同控制过程中，采用部分牵引力与制动力，延长牵引与制动力输出时间，有利于降低系统总体净能耗的结论。

除了上述基于提前计划列车运行速度曲线的方法，荀径等、宋晓美提出了一种通过检测牵引供电接触网（第三轨）电压，并在接触网电压升高时适当提高邻近列车运行速度的方法，以提高城轨列车再生制动能量使用效率，从而实现城轨列车的节能运行。作者设计的模型包括列车节能运行优化控制算法和牵引供电模型两个部分。模型通过牵引供电系统的直流潮流计算，获得列车网压，并建立了列车到站时间预测评估的元胞自动机交通流模型和需要调整的列车判断条件，避免了经过调整的列车加速后触发制动曲线。

3.面向多列车的节能系统

基于通信的列车自动控制（Communication Based Train Control，CBTC）系统中大容量、双向连续的车地通信，实现了对在正线运行的列车连续实时控制，也为面向节能的多列车协调控制、提高再生制动能量使用，降低系统总运行能耗提供了环境基础。

基于现有CBTC通信链路与交换数据、自律分散理论，笔者设计了一种多列车节能协调控制方案，如图5－29所示。该方案集成于现有CBTC系统框架体系内，工作于CBTC模式运行的正常运营场景，暂不适用于出现信号设备故障等需要降级转为后备模式或在辅助安全设施防护下的场景。

在图5－29中，最右侧虚线范围内确定了可参与多列车节能协调控制的列车范围。图中以ATS设备为界限，该设备右侧相邻方框内的设备为既有CBTC系统设备，CBTC设备之间的连接线表示通信与数据交换链路。其中，实线表示通过有线方式传输数据，虚线表示通过无线通信方式传输数据；其中短虚线连接线表示传输的数据内容与既有CBTC数据相同，点划线连接ATS与列车车载设备，该通信链路除了传输与既有CBTC系统相同的数据信息外，还附加传输多车协调控制信息。在ATS设备左侧为采用自律分散系统构架的多列车节能协调控制服务器群（节能服务器）。节能服务器采用分布式布置，根据线路、牵引供电系统、车辆和运行图等基础静态数据，以及ATS调度命令、列车载客质量、运行状态等动态信息，进行多列车协调控制的节能优化。

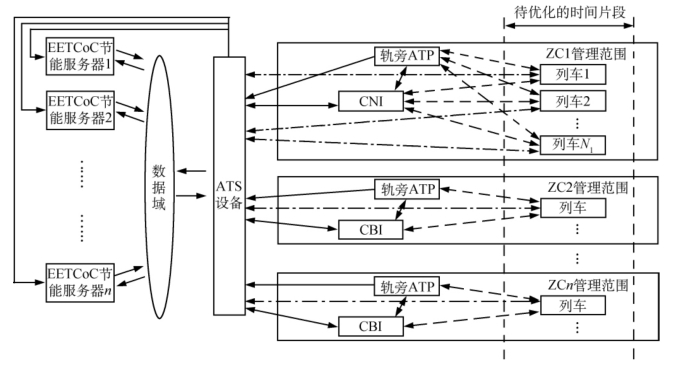
图5－29　多列车节能协调控制框架

节能服务器的数据通信链路均采用有线方式连接，主要分为两个方向：ATS设备至节能服务器的单向数据链路和节能服务器与数据域之间的双向通信。除此之外，ATS设备与数据域之间还存在双向通信。

ATS设备至节能服务器的单向数据链路：列车运行图数据。可以认为在正常运行的条件下，每日运行图均为制定的固定参数，在运营中基本不会发生变更，因此只需每日更新，无须在运营期间实时传输。

ATS设备至数据域的数据链路：抄送传输ATS下达的调度命令、可参与协调控制的列车信息，例如列车载客质量、运行状态等。可以认为此信息是时变的，需要以一定的刷新频率更新。

数据域至ATS设备的数据链路：ATS利用数据域内数据的CC码，获取经节能优化服务器优化得到的协调控制方案，包括参与协调控制的列车编号、各个列车协调控制开始的状态、协调控制持续时的控制输出等信息。ATS通过车-地无线通信系统，与调度命令等信息一同，发送给相应的车载设备。数据域至ATS设备链路的数据刷新率与所选择的优化时间片段相关，以一定的周期定时更新。

数据域至节能服务器的数据链路：利用数据域内的CC码，一种情况是节能服务器获得ATS设备推送至数据域的调度命令、可参与协调控制的列车信息，作为其优化计算的输入；另一种情况是节能服务器获得其他节能服务器计算的中间步骤数据，为节能服务器群分布式并行计算的数据交换。

节能服务器至数据域的数据链路：①发送该节能服务器计算的中间步骤数据，为节能服务器群分布式并行计算的数据交换；②发送列车协调控制优化结果。

除此之外，例如线路坡度、曲线、限速信息，列车最大牵引力／制动力、不同载重下基本阻力参数，列车电能与机械能各环节转化效率，供电分区信息、牵引供电系统电气参数等数据，将通过预先离线存储的方式，存储于各个节能服务器内，供优化计算时调用。

上述采用基于自律分散构架设计的多列车节能优化协调控制框架，体现了自律分散在线扩展、在线维护和在线容错的特点。由于各节能服务器都是平等独立的，通过自身存储的相同基础数据和各自通过CC码与数据域的数据交换，领取计算任务并返回结果，易于实现优化计算能力的在线扩展与在线维护；待优化的列车范围也是随着运行图的计划、实际运营情况而不断变化，并通过ATS将数据传递于数据域内。对于在线容错方面，笔者认为可以将其定义为在线包容不参与协调控制的列车这一特性。因为对于多列车节能优化协调控制而言，为了达到系统最优，并不一定是所有在待优化时间窗片段范围内的列车都需要参与协调控制，而是根据优化服务器计算的结果，选择相应的列车，在计划的状态范围内进行协调控制。