三相滞环电流比较控制在高速铁路同相供电中的应用

与空间电压矢量控制相结合，通过滞环电流比较控制和空间电压矢量实时切换，使电流误差限制在滞环宽度以内。这种控制策略响应速度快，且具有很好的健壮性，适合应用于电气化铁道同相供电平衡补偿系统。它主要有两大类：不定频滞环电流比较空间电压矢量控制[144，145]和定频滞环电流比较空间电压矢量控制。以下介绍不定频滞环电流比较空间电压矢量控制，定频滞环电流比较空间电压矢量控制将在下一节介绍。

1．滞环电流比较控制规则

参照单相变流器双滞环电流比较控制原理，可以直接给出三相变流器滞环控制规则：

规则1，当电流误差| Δ I|＜ h时，保持开关状态不变，以减小开关频率，减小开关损耗；

规则2，当电流误差h≤Δ I|＜ h+Δh时，调整开关状态尽可能使电流误差| ΔI |以最小速度减小；

规则3，当电流误差ΔI|≥h+Δh时，应调整开关状态使电流误差| ΔI |以最快速度减小，以确保电流跟踪效果。

假定电流误差超出边界，为了使电流误差绝对值减小到边界以内。以开关切换时刻为时间起点，起始点t=0的电流误差矢量记为ΔI0，各相分量分别记为Δia0、Δib0、Δic0；切换后t时刻的电流误差矢量记为ΔI，其各相分量分别记为Δ ia、Δ ib、Δic。根据式（6.35）可得某一相的电流误差为

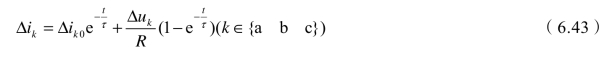
其中，τ=L/ R。由式（6.43）可以看出任意时刻的电流误差由两部分构成：一是由于开关切换时刻电流误差产生的响应分量，其绝对值随时间而减小，如式（6.43）等号右侧第一项所示；另一部分是由于电压误差不为零产生的响应分量，其绝对值随时间而增加，如式（6.43）等号右侧第二项所示。为了保证开关切换后使电流误差减小到边界以内，则Δuk应与Δik0符号相反，即，如果Δik0＞0，则应使Δuk＜ 0；如果Δik0＜ 0，则应使Δuk＞0。

式（6.43）写成矢量形式为

从式中可以看出，当ΔU与ΔI0同向时，ΔU将使电流误差ΔI的模值增大；而当ΔU与ΔI0反向时，ΔU将使电流误差ΔI的模值减小。

若式（6.44）中，τ=0.01 s，|ΔU/ R |=2|ΔI0|=2时，可计算得到电流误差与ΔU、ΔI0的关系曲线，如图6.33、图6.34所示。图6.33、图6.34分别为ΔU与ΔI0同向和反向时的电流误差变化曲线，其中实线对应初始电流误差曲线，即对应式（6.44）等号右侧第一项；虚线是开关状态对电流误差影响曲线，即对应式（6.44）等号右侧第二项。标注“*”的曲线代表在初始电流误差和开关的双重作用下实际电流误差变化曲线。从图6.33和图6.34可以更清楚地看出，调整开关的状态使ΔU与ΔI0同向时，将使电流误差绝对值进一步增大，说明开关状态调整方向是错误的；调整开关的状态使ΔU与ΔI0反向时，将使电流误差绝对值迅速减小，不到4 ms时电流误差变为零。

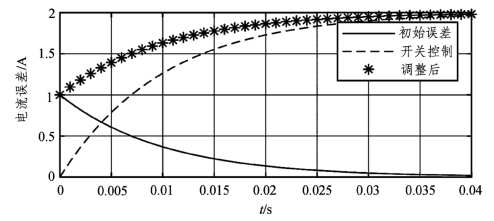
图6.33　当ΔU与ΔI0同向时的电流误差曲线

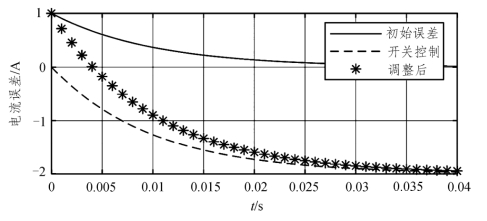
图6.34　当ΔU与ΔI0反向时的电流误差曲线

所以，为了减小电流误差，把电流误差控制在边界以内，则应调整开关使ΔU与ΔI0反向。若ΔU与ΔI0完全反向共线，令Δ I=0可求得

式（6.45）说明，ΔU的模值越大，则时间t越小，即ΔI模值下降为零的时间越短。因此，只要ΔU的模值足够大，就能在很短的时间内使ΔI的模值快速减小为零。减小的快慢与ΔU的模值大小有关。当h≤| Δ I|＜ h+Δh时，为了减小开关频率，应选择与ΔI0反向的最小模值ΔU ；当| ΔI|＞h+Δh时，为了提高跟踪效果，应选择与ΔI0反向的最大模值ΔU。

由于可供选择的空间电压矢量只有八个，所以通常情况下ΔU不可能完全与ΔI0反向共线，假定ΔU=-m ΔI0R ∠θ，其中，m为正比于ΔU与ΔI0模之比值的一个常数，θ 为ΔU与ΔI0反向夹角，如图6.35所示。

将ΔU=-m Δ I0R ∠θ代入式（6.44）可得

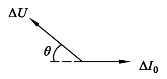
图6.35　电压电流误差矢量之间的关系

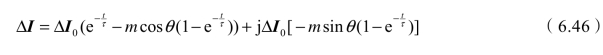
由式（6.46）可以看出，ΔI由实部和虚部两部分组成。只要m cosθ 足够大，也即ΔU的模值足够大且与ΔI反方向的夹角θ 足够小，实部绝对值就能在较短时间内降到足够小；虚部绝对值随时间而增大，而且θ（θ 为锐角）越大则其绝对值越大。所以为了使ΔI的模值减小到一定值，必须使ΔU与ΔI0反向夹角θ 足够小，也就是选择开关状态应使ΔU与ΔI0尽可能接近反向共线；如果想提高电流的跟踪速度，则应选择与ΔI0反向、模值足够大ΔU；如果想减小开关频率，则应选择与ΔI0反向、模值小的ΔU。

2．最优开关状态的选择(www.xing528.com)

根据空间电压矢量原理，只要知道ΔI、U*落入的空间区域，就可以确定开关的切换状态。三相空间电压矢量将U*所在的矢量空间自然划分成六个三角形区域，分别记为Ⅰ～Ⅵ区，对应的三相坐标轴分别为a，b，c，如图6.36（a）所示。同样，为了确定ΔI的空间位置和便于判别Δia、Δib、Δic的极性，也将ΔI所处的空间划分成六个区域，并记为①～⑥区，如图6.36（b）所示，其中h代表电流滞环宽度。根据三相坐标轴a、b、c的相对空间位置可以看出，电流矢量空间六个区域的位置相当于空间电压矢量构成的六个三角形顺时针旋转了30°。

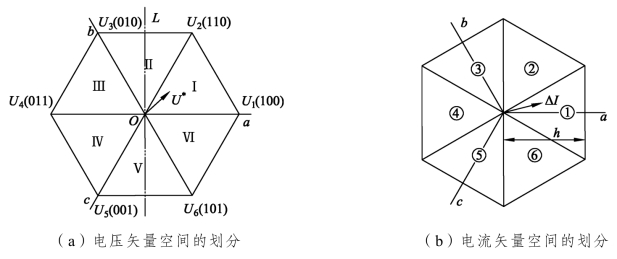
图6.36　电压、电流矢量空间区域的划分

根据ΔI0、U*落入的区域，可以找到能够产生与ΔI0反向的最小模值ΔU和最大模值ΔU及其对应的空间电压矢量Uk。以ΔI落入①区为例，假定U*落入Ⅲ区，如图6.37所示，从各空间电压矢量顶点向U*矢量顶点引线，则线段长度就是各空间电压矢量所对应的ΔU的模值。与ΔI0反向的ΔU共有四个，分别是ΔU0，7、ΔU1、ΔU2、ΔU6，其中ΔU1是最大的，ΔU0，7是最小的。只要U*落入Ⅲ、Ⅳ区任何位置，ΔU0，7就是与ΔI0反向的最小电压误差矢量，ΔU1就是与ΔI0反向的最大电压误差矢量，对应的空间电压矢量分别是U0，7和U1；当U*落入Ⅰ、Ⅵ区任何位置，与ΔI0反向只有ΔU1，ΔU1即是最小也是最大电压误差矢量；当U*落入Ⅱ区时，与ΔI0反向的最小电压误差为ΔU2，最大电压误差是ΔU1；当U*落入Ⅴ区时，与ΔI0反向的最小电压误差为ΔU6，最大电压误差是ΔU1。ΔI0与U*落入不同区域时开关状态选择如表6.5所示。

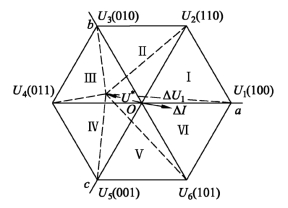
图6.37　N=4落入Ⅲ区时的电压误差矢量

表6.5　ΔI0落入不同区域时开关状态选择

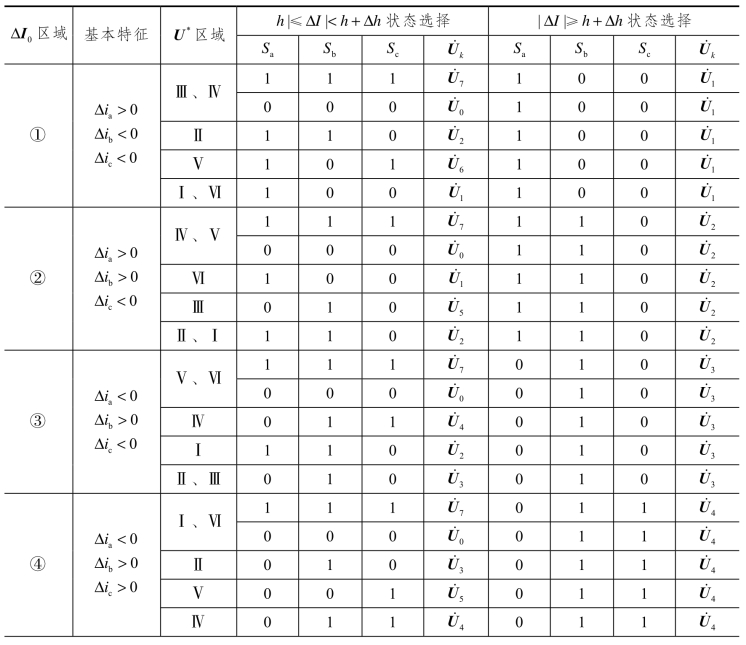
续表

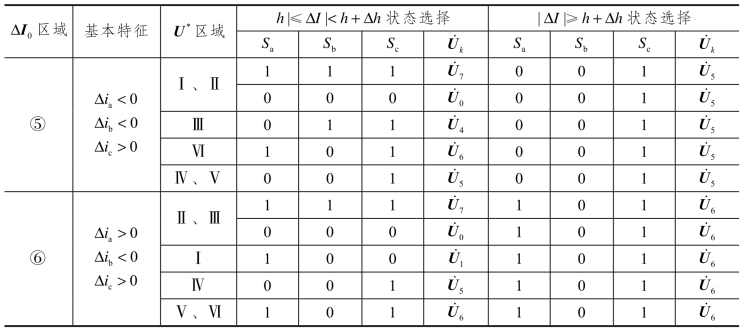
所以，如果知道了　U*、ΔI0落入的区域，按照表6.5就能确定开关的最优控制状态。

3．U*与ΔI落入区域判别

U*落入区域判别已在前面阐述，下面仅介绍ΔI落入区域判别。定义：

式中

那么ΔI所处的区域逻辑关系为

表6.6　ΔI区域判别

注：“＋”表示Δij＞0，“－”表示Δij＜ 0，其中j ∈{a b c}。

式中RΔI（1）～RΔI（6）为ΔI对应落入区域1 ～6的逻辑变量。若ΔI落入X区，则RΔI（X）=1，否则RΔI（X）=0，其中X的取值为1～6的数字。例如，当ΔI落入①区时，通过式（6.49）逻辑运算可得RΔI（X）=1；当ΔI落入区域①以外时，RΔI（X）=0。

4．不定频滞环电流比较控制原理

不定频滞环电流比较控制原理如图6.38所示。各相期望电流指令信号与变流器实际输出电流反馈信号，经滞环比较器，按照式（6.47）、式（6.48）确定输出状态值Xa、Xb、Xc；期望电压指令信号经区域判别单元输出状态值Dab、Dbc、Dca。最终按照状态选择表6.5确定开关的状态矢量，输出合适的空间电压矢量Uk，即最优的开关状态。在Uk的作用下可以使变流器三相输出电流逼近三相期望电流。

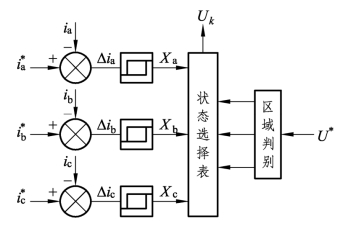
图6.38　滞环电流比较控制原理