高速铁路单相变流器滞环状态控制

1．电压误差与电流误差

基于平衡变压器构成的同相牵引供电系统，平衡变换装置由两个背对背的单相变流器构成，如图3.12所示，两个变流器可以相对独立进行控制，所以从控制方法上讲，属于单相变流器控制，其等效电路如图6.1和图6.2所示，对应ac或bd相变流器，有：

式中　L、R、e——系统等效电感、电阻和电源电势，其中e代表eac或ebd；

u、i——变流器输出电压（ uac或ubd）和输出电流。

若设u*、i*为变流器输出电压、电流的期望值，则

将式（6.21）和式（6.20）相减得

其中，Δi=i*-i、Δu=u*-u分别为电流误差和电压误差。

由式（6.22）可知，电流误差 Δ i与电压误差 Δ u有关。改变 Δ u的大小，可以使电流误差 Δi增大或减小。通常在很短的时间内可认为u*恒定不变，因此电压误差主要是受变流器的输出电压也即开关状态的影响。因此，控制开关的状态可以控制电流误差的大小。

定义二值逻辑函数

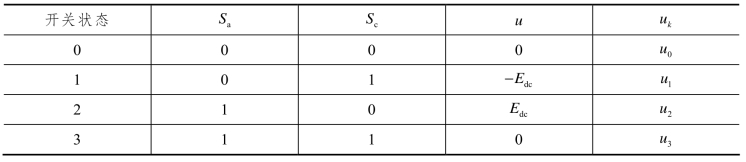
式中，m∈{a c}与桥臂对应，当m为a时，sa表示a桥臂的状态。单相变流器有两个桥臂，见图3.12两个桥臂的二值逻辑用sa、sc表示，对应共有四种状态三种输出电平，其对应关系如表6.1所示。

对应一组确定的开关状态，只能输出一种电平，所以，通常u ≠ u*，Δu=u*-u ≠ 0，如果不调整开关状态，那么电流误差 Δi绝对值必然会随时间而增大。为了将电流误差限制在规定的范围内，必须通过不断地调整开关状态才能实现。

表6.1　开关状态与输出电平（注：Edc为直流侧电压）

2．滞环控制原理与状态优化

滞环电流控制的目标是将变流器的输出电流与期望电流的误差控制在允许值范围以内，通常要求式中，h为电流误差允许最大值。根据式（6.24）可解析出以下滞环电流控制逻辑：

当| Δi | ＜h时，说明电流误差在允许范围内，应保持变流器开关的状态不变，以减小开关频率，降低开关损耗；

当| Δi | ≥h时，说明电流误差超过允许值，应调整变流器开关的状态，使电流误差绝对值减小到允许值以内。分两种情况：如果 Δi≥h时，则应调整变流器的开关状态，使 Δi减小；如果 Δi≤-h时，则应调整变流器的开关状态，使 Δi增大。

根据式（6.22），由于R很小，可忽略其影响，则Δu=LdΔi/dt，所以：当Δu ＞0，Δi随时间而增大；当Δu ＜ 0，Δi随时间而减小；当Δu=0，Δi保持不变。

当u*＜ 0，u *在[-Edc0]区域之内时，变流器开关可在状态“0”与状态“1”之间切换使u逼近u *。状态“0”时，u*-uac＜ 0，Δi随时间而减小；变流器为状态“1”时，u*-uac＞0，Δi随时间而增大。所以在状态“1”与状态“0”之间切换，可以将电流误差控制在允许范围以内。同样，在状态“1”与状态“2”之间切换，也能将电流误差控制在允许范围以内，但一次需要切换两个桥臂开关，加之状态“2”比状态“0”的电流误差变化率大，因此开关频率也会相应增高。

当u*＞0，u*在[0Edc]区域之内，变流器开关可在状态“0”与状态“2”之间切换使u逼近u*。状态“0”时，u*-uac＞0，Δi随时间而增大；状态“2”时，u*-uac＜ 0，Δi随时间而减小。所以在“状态0”与状态“2”之间切换，可以将电流误差控制在允许范围以内。同样原因，在状态“1”与状态“2”之间切换，也能将电流误差控制在允许范围以内，但会增加开关频率。

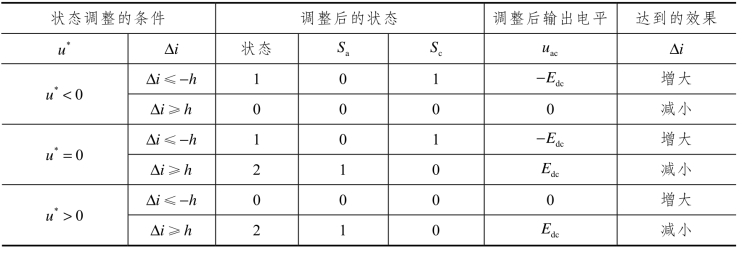
综合以上分析，可得到变流器状态优化规则，如表6.2所示。(www.xing528.com)

对表6.2表6.2变流器状态控制规则需要做几点说明：

（1）由于状态“0”与状态“3”输出电平相等，所以在状态选择时，只要不导致开关频率增加，选择任何一个状态效果是等价的。

（2）当u*=0时，状态“0”恰好使变流器输出u=0=u*，电流误差既不增大也不减小，如电流误差在允许范围以内，也就没有必要调整开关的状态了。但是由于误差等原因，实际上变流器输出电流仍然会偏离期望值，这就需要根据表6.2表6.2变流器状态控制规则调整变流器的开关状态。

表6.2　变流器状态控制规则

3．双滞环状态优化控制

状态优化是基于期望电压u*所落入的区域来确定下一步开关的状态。根据式（6.21），如果已知i*就可以确定u*。但是，对于电气铁道供电系统，参数L、R是动态变化的，具有不确定性，需要实时估算；更重要的是式（6.21）与实际系统模型总存在一定的误差，所以，即使根据式（6.21）能够准确估算各参数，也无法准确确定期望电压u*，或者说是计算得到的期望电压u*，与实际值总会存在较大的误差，难以满足实际要求。如果期望电压u*未知或不能准确确定时，又该如何优化开关的状态呢？我们可以根据电流变化率的增量来判定。

若令 Δ t为t与t0时间差值，即Δt=t -t0； Δ i、Δ i0分别为t、t0两个时刻的电流误差。若Δ t足够小，则d Δi/d t≈（Δi-Δi0）/Δ t，并假定系统电阻R很小可忽略，则式（6.22）变为

从式（6.25）可以看出，如果Δi-Δi0＞0，则说明Δu ＞0；如果Δi-Δi0＜ 0，则说明Δu ＜ 0。所以，如果知道了前后两个不同时刻电流误差的差值，就可以判定输出电压与期望电压的相对大小，据此可以确定开关的调整方向。根据这一原理可构造出双滞环电流比较状态优化控制框图，如图6.29所示。

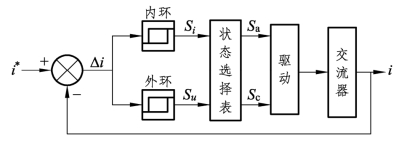
图6.29　双滞环状态优化控制框图

图中Si、Su分别为内环和外环比较器输出状态值。内外滞环比较器输出状态值与电流误差值关系，如图6.30所示，粗实线为内滞环，其滞环宽度为2h；细实线为外滞环，其滞环宽度为2h1，h1＞h。

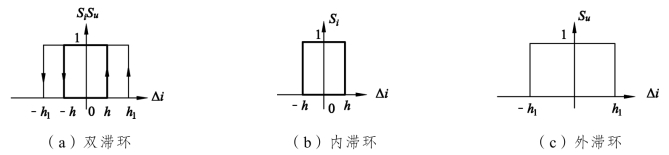
图6.30　内外滞环比较器输入输出特性

对于内滞环，当 Δi≥ h时，Si=1；当 Δi≤ -h时，Si=0；当| Δi|＜ h时，维持原状态。

对于外滞环，当Δi≥ h1时，Su=1；当Δi≤-h1时，Su=0；当| Δi|＜ h1时，维持原状态。

状态选择表是根据Si、Su的状态来确定开关的切换状态Sa、Sc的值，可按以下关系式确定：

在各种状态下，开关状态的选择如表6.3所示。

表6.3　双滞环电流比较状态选择表

分析可知按照以上切换规则，通常 Δi将被限制在内滞环范围内，也即 -h≥ Δi ≤ h ；只有当开关处在“1”态，而u*＞0，以及开关处在“2”态，而u*＜ 0时，Δi才会越出内滞环边界，但 Δi不会越出外滞环范围以外。

控制方法特点是：

（1）滞环比较器每翻转一次，调整一次开关状态，且一次只调整一个桥臂开关状态，因此开关次数少。

（2）每次调整开关状态，总试图使误差减小，电流误差不会超出滞环边界。