高速铁路同相供电技术实现任意电压波形

方波逆变器将直流电变成了交变的方波，实现了直流到交流的转换。但是不可调的固定方波逆变器存在两个突出的问题：① 输出的电压大小、频率、相位不可调；② 输出电压谐波次数固定，谐波含量极高，波形质量差。虽然单相全桥逆变器可以通过脉冲宽度调整输出电压的幅值和谐波含量，但调整幅度十分有限，无法满足实际需要。同相牵引供电系统期望补偿电流大小和相位都将随负载改变而动态变化，因此不可调的方波逆变器，无法满足同相供电平衡补偿的要求。PWM脉宽调制技术和多电平技术可以有效解决这些问题。

PWM脉宽调制技术是对逆变器开关管的导通与关断进行有规则的控制，使其输出一系列幅值相同而宽度不等的矩形脉冲序列，用这些脉冲序列去逼近一个所期望的电压或电流信号。为什么一系列矩形脉冲可以逼近任意一个信号？可以从作用效果和波形质量两个方面来理解：一是冲量相等（也即面积相等）而形状不同的两个窄信号作用于惯性系统，其效果基本相同。而任意信号与横轴围成的面积总可以等效为一系列矩形脉冲信号的面积之和。所以从作用效果上来看，任意信号可以用一系列矩形脉冲信号逼近。二是从波形的质量来看，一系列矩形脉冲信号与所逼近的信号也基本相当；若用傅里叶变换进行分析，二者的频谱，在高频段略有差异，其他频段基本相同；若将二者展开成傅氏级数，则二者基波基本相同，高次谐波含量略有不同。

1．正弦脉宽调制（SPWM）

借用通信中调制波与载波的概念，用正弦波作为调制波，以高频三角波（或锯齿波）作为载波，比较二者的大小，以此控制输出脉冲的宽度，从而产生一系列幅值相同宽度不同的脉冲。图6.13为正弦脉宽调制电路。三角波的载波电压uc与正弦调制波电压us进行比较，当us＞uc时，比较器输出电压为高电平；而当us＜ uc时，比较器输出电压为低电平。输出脉冲的宽度正比于正弦调制波的函数值。图6.14为正弦脉宽调制波形示意图，其中图6.14（a）黑实线为50 Hz正弦调制波，细实线为550 Hz三角载波；图6.14（b）为PWM正弦脉宽调制波形，各脉冲宽度不一。正弦调制波函数值越小，脉冲宽度越窄；正弦调制波函数值越大，脉冲宽度越宽。改变三角载波频率就可以改变一个周期内脉冲数。当三角载波频率增加时，一个周波的脉冲数增加，而脉冲数越多逼近调制波的效果也越好，但同时要求开关的频率越高，开关损耗也越大。

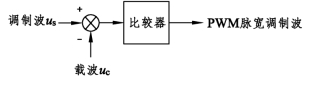
图6.13　正弦脉宽调制电路

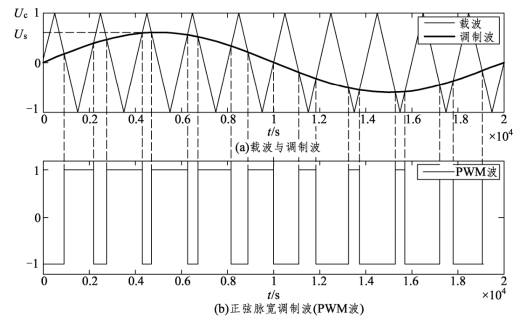
图6.14　正弦脉宽调制波形

当三角载波的频率为1080 Hz，调制波为50 Hz纯正弦波，调制度为M=0.9（M=Us/Uc，其中Us、Uc分别为调制波和载波的幅值）时，由正弦脉宽调制产生的PWM波去控制图6.8所示的单相半桥逆变电路，单相半桥逆变电路直流侧电压E=20 V，则输出电压波形及其频谱如图6.15所示。根据电压型逆变器的特点其输出电压波形在理想的情况下与调制波相同。从图6.15可以看出，输出波形中含有谐波，且谐波主要集中在开关频率附近，如果用滤波器滤除高次谐波，则除幅值不同外，输出电压的波形是与调制波形完全相同的纯正弦波，所以逆变器的输出电压波形可以逼近调制波波形。

图6.14和图6.15所示的三角载波、正弦调制波和PWM波在任何半个周期内均有正、负极性的电压交替出现，称这种调制为双极性调制。双极性调制的优点是可以有效提高直流电压的利用率，但明显增加了开关的频率和损耗，PWM波谐波成分也有所增加，同时由于同一个桥臂上两个开关器件始终是轮流交替通断，而一般开关器件的关断时间总比开通时间长，为避免两个开关同时导通的“短路故障”，必须增加延时触发环节。

与双极性调制相对应，在半个周期内每个桥臂只有上或下一个开关器件作通断控制，另一个开关器件关断，调制波和载波均只有单一的极性，这种调制方式称为单极性调制。如图6.16所示，逆变器输出PWM波也是只有单一的极性，图示PWM波的负半周是通过倒相得到的。

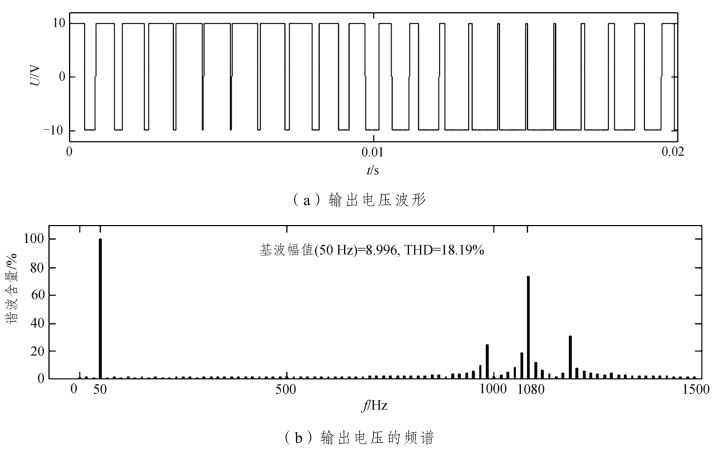
图6.15　PWM调制单相半桥逆变器的输出电压波形及频谱

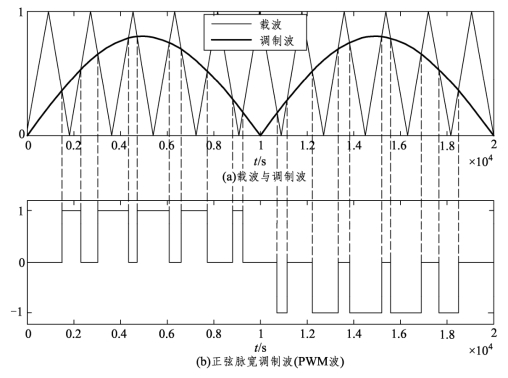
图6.16　单极性正弦脉宽调制

单极性调制的优缺点与双极性调制正好相反，由于同一个桥臂上的一个开关器件在半个周期内开通和关断时，另一个开关器件始终是关断的，因此，可以省去延时触发环节，可避免因延时环节引起的失真，同时减小了开关频率、损耗和输出波形的谐波含量。但单极性调制会因为负载的变化，同一桥臂上两个开关器件会同时出现关断状态，这时输出电压不确定，会对电压波形产生影响。

用正弦脉宽单极性调制产生的PWM波去控制图6.9所示的单相全桥逆变器，输出电压波形如图6.17和图6.18所示。图6.17三角载波的频率为1 080 Hz、调制波为50 Hz纯正弦波、相位为0°、调制度为M=0.9时的输出电压波形及其频谱。图6.18中三角载波的频率为1 080 Hz、调制波为50 Hz纯正弦波、相位为30°、调制度为M=0.8时的输出电压波形及频谱。为了便于比较，两种情况输出电压基波分量分别绘于图6.19。

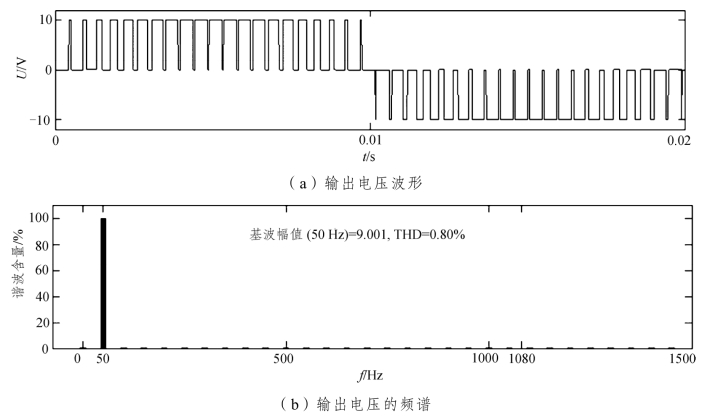
图6.17　M=0.9时单相全桥逆变器输出电压波形及频谱(www.xing528.com)

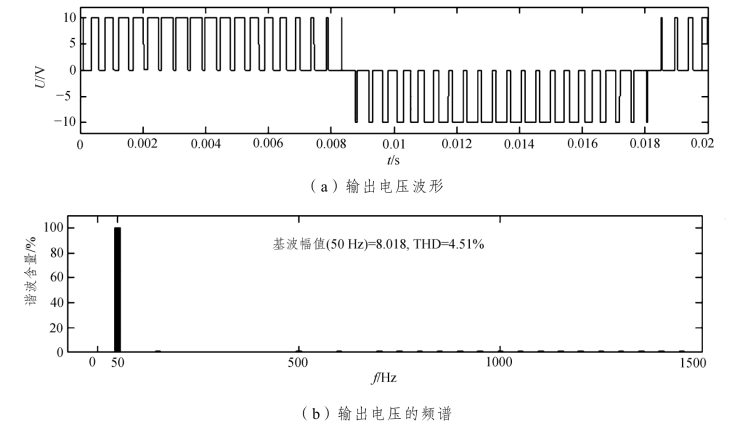
图6.18　M=0.8时单相全桥逆变器输出电压波形及频谱

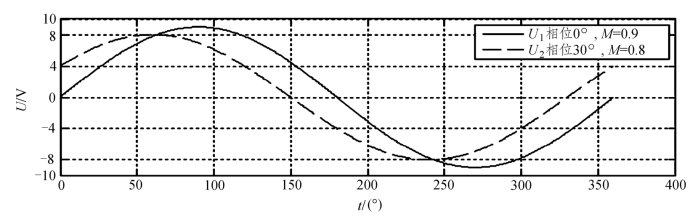
图6.19　调制波形改变时逆变器输出基波电压波形及频谱

观察图6.17、图6.18和图6.19可以看出：

（1）单极性调制谐波含量很小，图6.17和图6.18输出电压波形的谐波含量只有0.8%和4.51%。

（2）改变调制度，也即改变调制波与载波的相对幅值，则输出电压波形幅值将成比例改变。如图6.17和图6.18所示，调制度为M=0.9时，输出电压基波幅值为9.001 V；而当调制度为M=0.8时，输出电压基波的幅值为8.018 V。

（3）改变调制波的相位，则输出电压的相位也相应改变。如图6.19所示，当调制波相位为0° 时，输出电压基波的波形对应图中实线U1，其相位为0°；而当调制波相位为30° 时，输出电压基波的波形对应图中虚线U2，其相位为30°。比较图6.18（a）与图6.17（a）输出电压波形，也可以看出输出电压相位随调制波相位的变化情况。

如果改变调制波的频率，输出电压波形该是怎样变化呢？当在其他条件不变的情况下，将调制波的频率改为250 Hz时，输出电压波形及其频谱如图6.20所示。

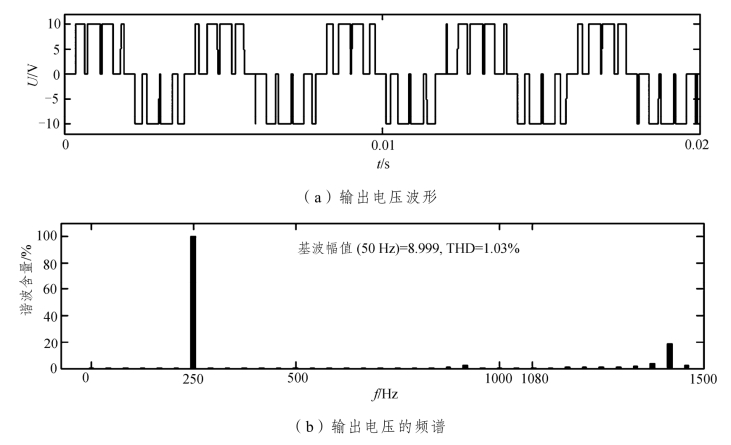
图6.20　调制波为250 Hz时输出电压波形及其频谱

由图可见，输出电压波形中除250 Hz外其他频率成分很小几乎可以忽略。也就是说输出电压波形相当于一个250 Hz纯正弦波形。

综上所述，当三角载波不变的情况下，改变调制波的幅值时，输出电压基波的幅值也成比例改变；改变调制波的相位和频率时，输出电压基波的相位和频率也相应改变。当开关频率足够高时，输出电压的波形就相当于放大一定比例的调制波形。

2．同步调制与异步调制

假定载波的频率为fc、调制波的（基波）频率为fs，则二者之比N=fc/fs称为载波比。不管调制波的频率如何变化，都始终保持载波比N不变，也就是保持载波信号的频率与调制波的频率同步变化，从而使载波比N为一常数，这种调制方式为同步调制；载波信号和调制波信号不保持同步关系的调制方式称为异步调制。

同步调制输出PWM波形稳定，正、负半周完全对称，尤其是在开关频率较低时保持输出波形的对称性，对于要求对称的系统是十分重要的。如三相对称系统，要求三相互差120°，这时只要取载波比为3的整数倍，就能使三相电压完全对称。在双极性调制时为保证每相波形的正、负半波对称，载波比必须是奇数。由于左右半波对称，输出波形中不含偶次谐波。为了使每半周的输出脉冲数在任何时刻都不变，因此，输出频率较低时，相邻两脉冲之间间距必然增大，输出波形的谐波会显著增大。由于载波周期必须随调制波周期连续改变，需要频率跟踪环节，也增加了控制技术的难度。

异步调制中载波比N不是常数，调制波频率改变，但载波的频率始终不变，由此可以提高低频段载波比。相当于输出电压半个周期内的脉冲数随输出频率的降低而增加，降低了输出电压中的谐波。但是，由于载波比是随调制波的频率不断变化，也就无法保证输出电压波形正负半波的对称性，对于三相系统，也就无法保证载波比始终是3的倍数，从而难以保证三相输出波形的对称性。

为了各取所长，通常将同步调制与异步调制结合使用，在一定频率范围内，采用同步调制，保持输出波形对称性；而在频率较低时采用异步调制，使载波比分段增加，来降低低频段输出电压的谐波。这样既发挥了同步调制的优势，又吸取了异步调制的优点，这就是分段同步调制。一般是将整个变频范围划分成若干频段，在每个频段保持载波比恒定，而对不同的频段取不同的载波比。高频段可采用相对较低的载波比，而在低频段采用相对较高的载波比。