基于最佳负载模型的检测方法

由式（4.19）可知，确定最佳负载模型的补偿电流的关键是计算G，直接计算G需要积分一个周期，数据窗过长，实时性不好。在这里采用恒定量分离法来求取G，再根据式（5.19）可计算出广义有功电流，如图5.16所示。

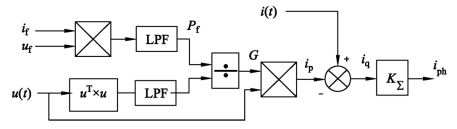
图5.16　基于最佳负载模型的检测法

根据前述Fryze检测方法知，if（t）与uf（t）的乘积中含有直流量和交流量两部分，用截止频率低于交流量最低频率的低通滤波器，可得到负载有功功率Pf。同样uT（t）u（t）中也有直流量和交流量两部分组成，低通滤波器输出恰好是其一个周期积分值。由此可以推得，图中ip就是牵引侧广义有功电流，而iph就是期望补偿电流。

以图3.8（a）单台变压器式同相AT牵引供电系统为例，假如三相等效星形电压为

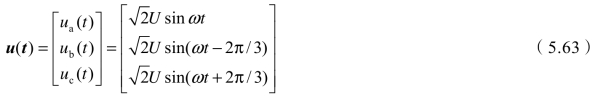
负载接于ab相间，所以负载端口电压为

式中，ψf为负载的接线角，在此ψf=-3 0°，为牵引网电压。假设负载电流中有谐波，为

式中，Ifn、φfn分别为n次谐波电流的有效值和初相角，其中，n=1时代表基波的量值。根据图3.8（a）可写出

将u（t）、i（t）、uf（t）、if（t）作用于图5.16对应输入端口，则

式中，为恒定直流量，等于负载的有功功率；为交流量。经滤波后可得Pf。(www.xing528.com)

所以图5.16中ip（t）=Gu（t）。根据定义iq（t）、iph（t）应分别是广义无功电流和期望补偿电流。从式（5.68）还可以看出，当三相电压完全对称时，uTu中只有直流量，所以图5.16中uTu通道并不需要LPF低通滤波器。

当系统三相电压不对称（或者三相电压幅值不等或相位并非依次相差120°），式（5.63）变为

则

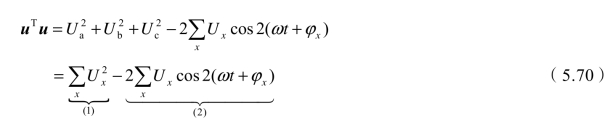
式中，x ∈{a b c}；其中第（1）项为直流量，第（2）项为交流量。所以图5.16中uTu通道必须有LPF低通滤波器。经低通滤波器后就只剩直流量。所以

式（5.71）说明，当三相电压不对称时，按照图5.16原理进行检测，则输出ip（t）的波形完全与三相电压的波形相同，其大小与三相电压成比例。所以，ip（t）正是最佳负载模型下的广义有功电流，那么iq（t）就是广义无功电流。如果完全补偿广义无功电流iq（t），则系统输出功率为即系统的输出功率正好等于负载的有功功率，这完全符合最佳负载模型的要求。

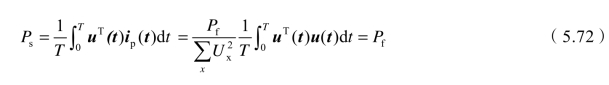
这种检测方法的特点是：

（1）无论电压是否对称和有无畸变都能得到准确的检测结果，检测结果总与最佳负载模型相符；该检测方法可用于检测最优补偿电流，此时KΣ=1，也可用于检测满意补偿电流，此时KΣ∈（0，1]。

（2）该检测方法不需要锁相环电路，不受电压波动的影响，因此即使被测电压发生剧烈变化，也能准确得出检测结果。

（3）当牵引侧三相（或两相）端口电压对称时（或在实际中忽略电压不对称），以上检测电路可做进一步简化，此时uT× u=uf×uf，因此可以减少运算量并简化电路，同时uTu通道可省去滤波环节。

（4）由于采用了滤波器，故系统仍有一定的延时[102]，延时长短与负荷所含谐波次数有关。对于电气化铁道一般仅有奇次谐波，若采用数字滤波器最长延时为10 ms。采用重采样技术可以进一步缩短延时[103]。