改进的高速铁路谐波与无功电流检测方法

1．单相电路有功电流分离检测法[91]

不失一般性，任设单相电网电压、电流如式（5.21）所示。电网电流可进一步写成：

将上式两边分别乘和，得

式中——式（5.25）右边乘后产生的各次交流量之和；

——式（5.25）右边乘后产生的各次交流量之和。

式（5.26）等式右端除I1cosφ1和I1sin φ1为直流量外其余都为交流量，所以分别用截止频率低于交流量中最低频率的低通滤波器滤波后并分别乘和，可得电网电流基波有功电流分量和基波无功电流分量。检测原理框图如图5.4所示。

如果仅检测谐波电流，可以不用锁相环电路，只需要一个与电压同频率的正弦信号发生电路。假定信号发生电路输出的正余弦信号与实际电压的相位差为任意值θ，即

图5.4　单相电路有功电流分离检测法

那么

所以图5.4中滤波器及其乘法器的输出，分别为

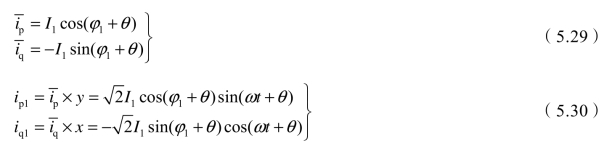
那么图5.4中的i1（t）为

可见，i1（t）正好等于系统电流is（t）的基波分量，那么最终输出ih（t）即为系统电流is（t）的谐波分量。

该检测方法的优点是不需要构造三相环节，电路简单，检测谐波可以不用锁相环，但检测有功和无功电流仍需要锁相环。检测电路的延时主要取决于滤波器的延时，而滤波器的延时与电网电流中的谐波有关。通常电气化铁道负荷电流只有奇次谐波，所以可以用10 ms延时的滤波器滤除式（5.28）中的交流量。

2．等效虚拟三相检测方法[100]

当前在有源电力滤波器中，应用最多的是基于瞬时无功功率理论的谐波与无功电流检测算法，这种算法具有动态响应速度快、检测精度高的特点，因此在工程设计中得到了广泛应用，但应用于单相电路时，存在很多问题有待进一步研究解决。文献[88]提出的基于瞬时无功功率理论的单相电路谐波与无功电流检测方法，存在构造三相的延时环节，需要众多的乘法器，算法复杂，计算误差大，调整困难，对电路的元件参数敏感，用于单相电路谐波检测时，其效果不理想[89]。文献[89]在三相ip-iq检测方法的基础上，提出了基于瞬时无功功率的虚拟三相法，它仍需要构造延时环节，降低了算法的实时性，同时构造延时的准确性对算法的检测效果影响较大，而构造三相时所需的理想的相位延时为 π/3，实际中很难精确实现，当延时相位与理想相位之间误差较大时，构造出的三相电流就变成了三相不对称电流（任意两相间的相位差不等于2 π/3 ），这必然会降低算法的检测精度。

可见构造延时环节是影响检测方法实时性和检测精度的关键因素。如果能够去掉不必要的构造延时环节，那么对于改善算法的性能具有重要意义。

1）等效虚拟三相检测方法的基本原理

前述基于瞬时无功功率理论的单相电路谐波与无功电流检测方法，由单相构造的三相系统满足对称性，而对称三相系统的各相电压（电流）相位互差120°，因此必须通过延时形成各相之间的相位差，这需要构造延时环节。为了去掉构造延时环节，必须打破构建对称三相电路的思路。

如果一个单相系统与一个三相系统对于负载（被测对象）是等效的，那么这两个系统向负载供出的电压和电流必然相同，对这个等效的三相系统实施谐波与无功电流检测，可以得到单相系统谐波与无功电流。

为不失一般性，设单相系统电压、电流为

图5.5　单相系统

对应的单相系统如图5.5所示。按照等效原理可以虚拟出与图5.5等效的三相系统，如图5.6所示。其中虚线部分是虚设的。其中图5.6（a）为虚拟三相四线系统，图5.6（b）为虚拟三相三线系统。注意虚拟三相系统，都是根据等效原理虚构的，没有任何构造环节和延时环节，虚拟系统的电压和电流都可以直接用单相系统电压和电流表示。可以证明，将虚拟系统的电压和电流加于图5.2所示的三相ip-iq检测电路时，或加于去掉三相构造环节的图5.3所示的单相电路瞬时无功功率检测电路时，电路输出就是被测单相系统谐波（或无功）电流。

图5.6　虚拟三相系统

由图5.6（a）所示的虚拟三相系统，可得如下电压、电流关系：

式中，K为检测修正系数，在此取K=3。将图5.6（a）中的ua和ia、ib、ic分别作为图5.2的输入。则由图5.2可得

将式（5.33）和式（5.32）代入上式得

式中，分别为ip、iq中的第n次交流分量。

式（5.35）中除直流量外，其他项都为交流量，经低通滤波器滤波后得

式（5.36）与式（5.19）完全相同，所以其后的输出也与ip-iq检测法完全相同。即

所以图5.2的输出iah=is-ia1。由于ia1为is的基波电流，所以图5.2的输出iah就是被测单相电路的谐波电流。

由图5.6（b）所示的虚拟三相系统，可得如下电压、电流关系：

根据电路等效原理，式中X可取任意值，但为了检测需要，取X=ubc=us，取K=1。再由图5.2可得

可见，图5.2电路输出iβ1与被测单相系统的基波电流仅相差倍数，所以就是被测单相系统谐波电流。如果将iα1与iβ1输出调换位置，则输出iah扩大3倍就是单相系统谐波电流。

在以上虚拟三相的基础上，如果断开图5.2电路的或通路，则可以检测单相系统基波有功、基波无功电流以及谐波与基波无功的和电流。

根据等效原理，同样也可以将单相系统虚拟为两相系统进行电流检测。图5.7就是将单相系统等效虚拟为两相系统。由图5.7所示的虚拟两相系统，可得如下电压、电流关系：

图5.7　虚拟两相系统

取K=2，将电压加于图5.2所示的电路ua，将两相电流、iβ直接加于图5.2所示的电路对应的iα、iβ输入端，相当于图5.2两边去掉αβ 坐标变换环节，直接简化为如图5.8所示检测电路。

图5.8　两相虚拟系统检测电路

根据图5.8可知，以下关系式成立：

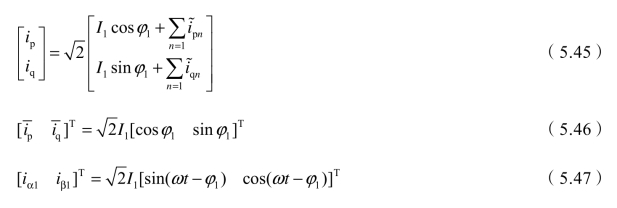
所以iah=is-ia1就是被测单相系统谐波电流。

可以证明，当只检测谐波电流时，不需要锁相环电路，只需通过信号发生器产生与电网电压同频率的正余弦信号即可，正余弦信号的相位不影响检测结果。

2）仿真分析

为了验证等效虚拟三相检测方法的正确性，以下基于matlab/simulink对三种虚拟检测方法分别进行了仿真，其中虚拟三相四线检测方法的仿真结果如图5.9和图5.10所示（其他方法的仿真结果与本方法相同，故以下略）。图5.9是谐波与基波电流检测的仿真结果。其中图5.9（a）是实际电网的电压与电流波形，为了使仿真符合实际情况和便于比较，假定电网电流波形是由基波和3、5、7、9、11、13次谐波分量组合而成，且谐波的幅值与次数成反比，谐波的相位为任意值。则电网电流可表示为

图5.9（b）为基波电流的检测结果与其实际波形，细实线为检测结果，黑实线为实际波形，从二者的波形来看检测结果与实际波形完全重合；图5.9（c）为谐波电流检测结果与实际波形，虚线为检测波形，实线为实际波形，二者波形完全重合。说明等效虚拟检测方法是正确的。(www.xing528.com)

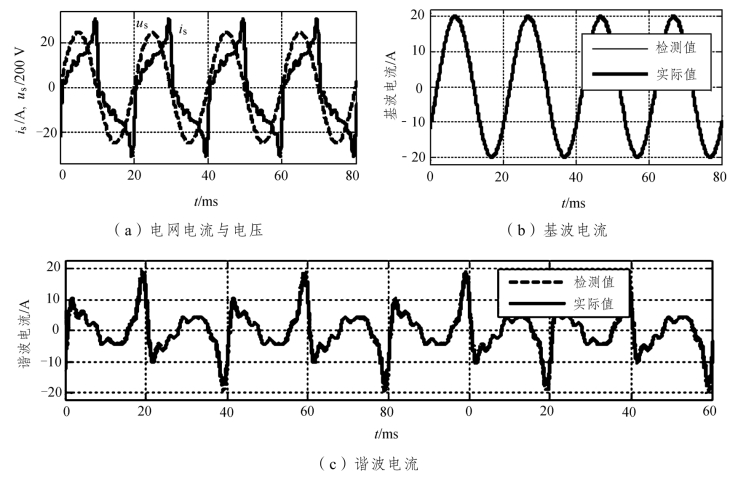
图5.9　检测结果与实际波形

图5.10是对检测方法的动态响应性能的仿真结果，假定电网电流为180° 方波，它与电源电压的相位差为36°。为便于观察假设在20～30 ms之间，is的幅值由8 A线性增加到20 A，us、is的波形如图5.10（a）所示。图5.10（b）、（c）、（d）分别为检测电路低通滤波器的输出、基波电流检测结果和谐波电流检测结果。可见无论从检测电路低通滤波器输出来看，还是从基波电流和谐波电流检测结果来看，都是在30 ms左右开始变化到40 ms结束并稳定。由此可见检测方法的动态响应性能较好。

图5.10　动态响应性能仿真结果

3）检测方法的特点

如前所述，基于瞬时无功功率理论的检测方法由于需要由单相构造三相的延时环节，因此引起了不必要的延时，降低了算法的实时性，同时也增加了检测电路的复杂性；理想延时在实际中很难精确实现，影响了检测精度。而等效虚拟三相检测方法不需要任何构造环节，因此消除了因构造环节带来的不良影响。与有功电流分离检测法相似，该检测方法的延时时间与滤波器有关，而滤波器的延时取决于要滤除的交流量的最低频率。对于电气化铁道采用10 ms延时的滤波器能够满足检测的精度和快速性的要求。

从功能和检测电路构成上看，基于有功电流分离的检测方法是等效虚拟三相检测方法的一种特例。以等效虚拟两相检测方法为例，根据iβ=0，经简化可得图5.4所示的检测电路，所以基于有功电流分离检测方法是无延时虚拟检测方法的特例。

单相和三相两种系统的谐波与无功电流检测方法有很多，它们既有联系又有区别。二者的区别决定了两系统的检测电路各不相同。等效虚拟三相方法，却可以使二者统一，至少可以将应用于三相系统的同一种检测电路，不用任何修改就能应用于单相系统，使单相和三相系统谐波与无功电流检测电路统一并标准化，有利于开发和推广应用，方便维护和调试。

这种检测方法的缺点是检测有功和无功电流时仍需要锁相环电路。

3．基于Fryze功率定义的检测方法[101]

与基于瞬时无功功率理论的检测算法相对应，也可以基于Fryze功率定义来构造谐波与无功电流检测算法。过去也有根据Fryze传统功率定义来构造检测方法方面的研究，但由此构造的检测方法需要很长的延时才能得出检测结果，存在实时性不好的缺点。

根据Fryze功率定义，瞬时有功电流为总电流的一个分量，其波形与电压完全一致，且一个周期内有功电流所消耗的平均功率和总电流消耗的平均功率相等；瞬时无功电流等于总电流与瞬时有功电流之差。由此根据图5.5单相系统可写出以下各式：

式中ip（t）、iq（t）—— is（t）的瞬时有功电流和瞬时无功电流；

P、G——平均有功功率和比例实常数，若U为电压的有效值，则G=P/U2。

由以上各式可知，只要得到平均功率P和电压有效值的平方U2，就可计算出G，再由式（5.49）和式（5.51）可求得电流的瞬时有功分量和无功分量。所以，基于Fryze功率定义实现无功电流检测的关键是求取P和U2两个量。下面分三种情况进行分析。

（1）当电压和电流中都含有谐波时。

仍设被检测的电压、电流如式（5.32）所示，则

式中，表示对下标n和m从1到∞的所有整数求和，以下同。

式（5.52）中除U2为直流量外，其他项都为交流量。所以，可用截止频率低于交流量中最低频率的低通滤波器对进行滤波，就能得到U2。

同理，电流瞬时值与电压瞬时值的乘积p为

同样式（5.54）中除P为直流量外，其他项也都是交流量。所以，可用截止频率低于交流量中最低频率的低通滤波器对p进行滤波，就能得到P。

求得P和U2后，就可按照Fryze的功率定义计算出无功电流。根据以上原理可构造出如图5.11所示的单相电路瞬时无功电流的实时检测原理框图。若定义，，则不难验证图5.11所示输出ip（t）、iq（t）分别为（推导过程略）：

显然瞬时有功电流ip（t）为谐波有功与基波有功电流之总和，它永远与瞬时电压成比例，波形完全相同，可称其为广义有功电流；瞬时无功电流iq（t）为谐波无功与基波无功电流之总和，可称其为广义无功电流。所以图5.11输出iq（t）可作为补偿无功时的参考量。

图5.11　无功电流的实时检测

检测广义无功电流时，不需要与被检测电压同相位的单位正弦信号，因此也就不需要锁相环电路及正弦信号发生电路。这是这种检测方法的优点。

值得注意的是图5.11中存在除法运算单元，但不影响检测。因为在正常运行状态下2U不为零，同时也不影响实现，尤其利用数字方式不难实现除法运算。

（2）当电压不含谐波，为时：

电流仍如式（5.32）所示，此时相当于

由式（5.53）和式（5.55）可得

将式（5.59）代入式（5.49）可得

显然瞬时有功电流ip（t）正是被检测电流的基波有功分量，并与瞬时电压成比例，与电压的波形相同，那么iq（t）便是谐波与基波无功电流之和。所以输出iq（t）可作为同时抑制谐波和补偿无功时的参考量。

（3）当电压为倍的单位正弦（余弦）信号时：

当，电流仍如式（5.32），根据式（5.53）和式（5.55）可得U2=1，P=I1cos（φ1+θ），图5.11输出ip（t）为

当，电流仍如式（5.32）时，根据式（5.53）和式（5.55）可得U2=1，P=-I1sin（φ1+θ），图5.11输出ip（t）为

式（5.61）和式（5.62）相加，得，i1（t）恰好为被检测电流中的基波电流分量，用is（t）减去i1（t）可得谐波电流。说明当us（t）为与实际电压同频率的正弦（余弦）信号时，图5.11检测电路稍加修改可用于检测谐波电流。由于初相角θ 是任意的，检测所得谐波电流与θ 无关，所以与实际电压同频率的正弦（余弦）信号可由正弦信号发生电路获得，因此检测谐波电流时不需要锁相环电路。

图5.12　电网电压及其频谱

图5.13　电网电流及其频谱

图5.12～图5.15分别为电网电压和电网电流的波形及其频谱。图5.12（a）、（b）是电网的电压波形及其频谱，图5.13（a）、（b）是电网电流波形及其频谱。电压与电流各次谐波含量如表5.1、表5.2所示。

表5.1　被测（电网）电压、电流各次谐波含量

注：实际电压、电流基波有效值分别为500 V、100 A。

表5.2　电流各次谐波有效值检测结果与实际值对照

图5.14（a）～图5.14（e）分别是广义无功电流、广义有功电流、基波有功电流、谐波＋基波无功电流、谐波电流的仿真结果，其中实线为实际波形，虚线为检测波形。由图可见由于检测误差很小检测波形与实际波形基本重合。各次谐波检测结果与其实际值如表5.2所示。由表5.2也可看出，检测结果中各次谐波量值与实际值非常接近。这说明本节提出的检测方法能够准确检测出谐波电流以及其他各量。

图5.14　谐波与无功电流检测结果

图5.15是对检测方法动态响应性能的仿真结果。假定电网电流为180° 方波，它与电源电压的相位差为36°。为便于观察假设在20～30 ms之间，is的幅值由100 A线性增加到200 A，is的波形如图5.15（a）所示。图5.15（b）、（c）、（d）分别为检测电路低通滤波器的输出、基波电流检测结果和谐波电流检测结果。可见无论从检测电路低通滤波器输出来看，还是从基波电流和谐波电流检测结果来看，大约在30 ms时开始变化，到40 ms结束并稳定。检测方法约有10 ms延时（这一延时是由滤波器引起的，考虑实际情况，应滤除的最低谐波次数为二次，若采用在一个最低次谐波周期内求平均值的数字滤波方法，可在1/2电源周期，即10ms后得到稳定准确的输出），可见检测方法的动态响应性能较好。

图5.15　动态响应性能仿真

基于Fryze功率定义的检测方法特点是：

（1）当电压无畸变时，检测基波有功、无功电流时，不需要锁相环电路；无论电压有无畸变，检测广义有功、广义无功和谐波电流时，也不需要锁相环电路。从这一点上讲，基于Fryze功率定义的检测方法优于其他检测方法。

（2）与基于瞬时无功功率的单相电路谐波与无功电流检测方法相比，基于Fryze功率定义的检测方法不需要由单相构造三相的构造环节，很好地解决了由于构造环节引起的问题。

（3）若通过正弦信号发生电路得到与电压同频率同相位的单位正弦（余弦）信号，由分析可以看出同样可以检测谐波、无功电流，此时由于U2=1，所以电路可以进一步简化。简化的检测电路与基于有功电流分离的检测方法相同，所以基于有功电流分离的检测方法可以看作基于Fryze功率定义的检测方法的一种特例。