同相供电关键技术与理论：正序功率与负序功率亮点

为不失一般性，设讨论的是n相系统（如果你认为三相系统好理解，也可直接令n=3），各相电压对称，基准侧参考电压为，k相电压滞后基准电压相位角为 φk，那么k相正序电流滞后于参考相正序电流相位角为φk，根据负序电流逆相序的特点，知k相负序电流将超前于参考相负序电流相位角 φk，所以k相电压和正负序电流可表示为

为表述方便，仍用X代表相别符号集合。

1．正序功率

（1）任意相的正序功率定义为该相的正序电压向量与该相的正序电流共轭向量乘积。由于系统电压完全对称，正序电压等于系统电压，因此，对任意的k ∈X，正序功率可表示为

式中，为k相的正序功率。

考虑k相电压及正负序电流与参考相之间的关系，以及同相供电系统只有一个端口接有负荷，根据式（1.109），可得对于任意的k ∈X，k相的正序功率为

式中，Sf=UfIf为负荷的视在功率，Uf、If为负荷端口的电压和电流有效值；为负荷的复功率。

由式（4.105）知，正序功率仅与负荷功率有关，与负荷接入的端口、负荷的接线角无关；各相正序功率相等，且恒等于负荷功率的1/n，即对于任意k ∈ X都有。

（2）总正序功率S+定义为各相正序功率之总和，即

将（4.105）代入式（4.106）可得

说明总正序功率恒等于负荷的总功率。

（3）总正序视在功率S+定义为各相正序视在功率之总和，即

根据式（4.105）和式（4.108），得

说明总正序视在功率恒等于负荷的总视在功率，即S+=Sf。

2．负序功率

（1）任意相的负序功率定义为该相的电压向量与该相负序电流共轭向量乘积，即对于任意k ∈X，有

式中，为k相的负序功率。(www.xing528.com)

将式（4.103）代入上式，并根据式（4.109），对于只有一个端口有负荷的同相供电系统，有

说明：各相负序功率的模值相等且等于负荷视在功率的1/n，其辐角与负荷的接线角和功率因数角有关。

当系统完全对称时总负序功率和各相负序功率都为零，所以负序功率必然是伴随不对称系统而产生的。将不对称系统变为完全对称的系统，也就意味着补偿装置提供了全部的负序功率。

（2）总负序功率S-定义为各相负序功率之和，即

将式（4.111）代入上式可得S-=0，即总负序功率恒等于零。这是因为负序电流不产生有功功率，负序功率总是在各相之间进行交换，说明负序的存在增加了系统的负担。

（3）总负序视在功率S-有两种定义：

根据分总视在功率定义，总负序视在功率为

将式（4.111）代入上式可得

根据集总视在功率定义，总负序视在功率为

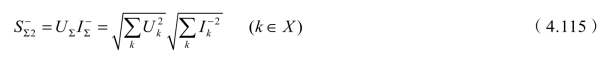
可以验证，当电压对称时，分总负序视在功率等于集总负序视在功率，即，两种定义结果一样。以下在没有特殊指明时，通常总负序视在功率是指分总视在功率。

式（4.114）说明：总负序视在功率恒等于负荷视在功率；总负序视在功率与变压器的接线方式、负荷接入的端口无关，因此，企图通过改变负荷的接线角（包括改变变压器的接线方式、采用特殊接线形式的变压器以及改变负荷接入的端口等）来改变负序视在功率的大小是徒劳的。

【例4.1】YN，d11接同相供电平衡补偿模型，如图4.2所示，bc相间接负荷，负荷的功率因数为cosφf=0.809，求负序功率。

解：以a相为参考，即（为等效星形a相电压），则负荷的接线角为ψf=90°，根据式（4.111），并注意此时n=3，可得

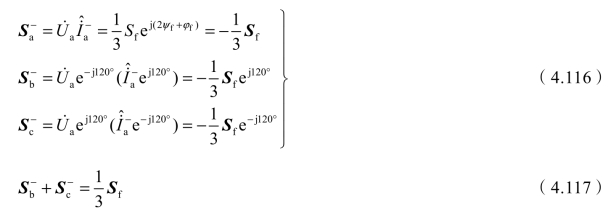
注意式（4.117）的右端为正，表示b、c两相即负荷端口bc相多承担了1/3的负荷功率；而式（4.116）中a相负序功率表达式的右端有一负号“－”，表示a相少承担了1/3的负荷功率。因此要想实现三相平衡就必须通过补偿装置将1/3的负荷功率从a相传向负荷的bc端口。

【例4.2】Scott接线同相牵引供电系统如图3.10所示，两相电压对称，负载接于M座（β 相），负荷的功率因数为cosφf=0.809，求负序功率。

解：以α 相为参考，即，所以负荷的接线角 ψf=90°，注意n=2、X={αβ}，则

注意式（4.118）右端的符号，其中α 相负序功率表达式右端有一个“－”号，表示α 相少承担了1/2的负荷（容量）功率；而β 相负序功率表达式右端为正，说明，β 相多承担了1/2的负荷（容量）功率。所以要实现各相负荷平衡就必须将1/2的负荷（容量）功率由非负荷相（α 相）传向负荷相（β 相）。

显而易见，任意星形n相系统，当只有一个端口有负荷时，接于负荷端口各相（负荷相）承担了负荷所需的全部功率，而非负荷端口的各相对负荷没有任何贡献。为了实现系统平衡，就必须将1/n的负荷（容量）功率从每一个非负荷相传向负荷端口。