高速铁路同相供电技术：最佳补偿电流

最优补偿电流是指达到最佳负载模型或波形畸变最小模型补偿目标时的期望补偿电流。

1．最佳负载模型

式中——补偿电流向量矩阵；——广义有功电流向量矩阵；——广义无功电流向量矩阵；

——补偿前系统输出电流向量矩阵。

对于任意k ∈X，则

式中、ik——补偿前系统k相输出电流向量和输出电流瞬时值；——k相的补偿电流、广义无功电流和广义有功电流向量；

ikph、ikq、ikp——k相的补偿电流、广义无功电流和广义有功电流瞬时值。

根据广义无功电流定义，补偿电流就等于广义无功电流。在最佳负载模型下，补偿装置必须提供全部的广义无功电流。

2．波形畸变最小模型

波形畸变最小模型与最佳负载模型不同，波形畸变最小模型的补偿目标是系统仅输出基波有功电流，所以

式中——波形畸变最小模型下（补偿后）系统的输出电流向量矩阵，也就是系统输出的基波有功电流向量矩阵；

——广义无功电流向量矩阵，是包括谐波、无功和负序的综合电流向量矩阵；

——补偿前系统输出的电流向量矩阵。

对于任意k ∈X，则

式中——k相的补偿电流、广义无功电流和基波有功电流向量；

ikph、iqk、ik1p——k相的补偿电流、广义无功电流和基波有功电流瞬时值。

3．牵引侧最优补偿电流

为不失一般性，假定待求量一侧，即基准侧（在此为变压器二次侧）为n相系统。n相电压完全对称，即n相电压大小相等相位互差2 π/n，用u（t）代表n相等效星形瞬时电压矩阵，基准侧基准电压为；负载电流只有基波电流，负载的功率因数角为 φf=φ1，可令负载电压和电流瞬时值为

式中　ψf——负载端口电压滞后基准电压的相位角，称为负载接线角，且滞后为正；

φf——负载的功率因数角，则负载所消耗的有功功率Pf=UfIfcosφf。

根据以上假设，有

根据式（4.19）可得基准侧广义瞬时有功电流矩阵为

将Pf=UfIfcosφf、Kf=Uf/Ux代入式（4.60）得

式中，u*（t）为基准侧的单位瞬时电压矩阵，u*（t）=u（t）/Ux。

作为特例，若求牵引变压器二次侧三相系统的广义瞬时有功电流，基准电压为，并假设三相电压对称，则三相等效星形电压瞬时值可表示为

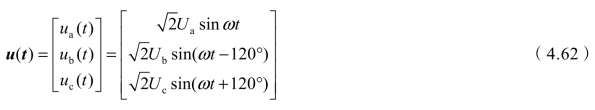
则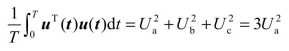。根据式（4.19）可得基准侧的三相广义瞬时有功电流为

将Pf=UfIfcosφf、Kf=Uf/Ua代入式（4.63）可得

对于两相系统，若以变压器次边为基准侧，以α 相电压为基准电压，即，则Kf=Uf/Uα，根据式（4.19）可求得变压器次边两相广义瞬时有功电流为

最佳补偿电流、广义瞬时无功电流为(www.xing528.com)

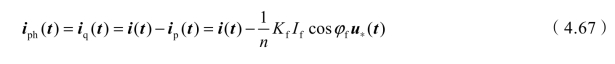
1）V，y-55接线

参照图3.4所示的接线方式，有

此时，基准侧三相电压u（t）为等效三相星形电压，如式（4.62）所示；基准电压，，代入式（4.67）可得牵引侧三相最佳补偿电流为

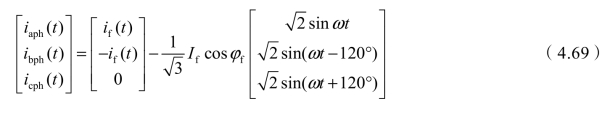
2）V，x-55接线

接线原理如图3.5所示，由图可得两端口电流以及补偿电流之间的关系：

可以推得补偿电流iaph（t）、icph（t）与式（4.69）相同。

3）单台YN，d11接线

对于图3.8（a）接线方式，有

基准侧三相电压u（t）为等效三相星形电压，仍假定如式（4.62）所示；基准电压，，代入式（4.67）可得

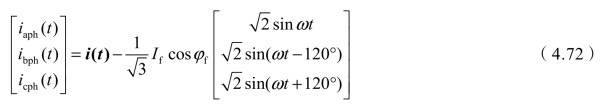
对于图3.8（b）：

基准电压，代入式（4.67）可得

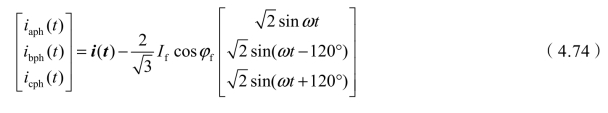
对于YN，d11接线，三角侧的等效星形电压将领先于原边电压30°。通常以原边A相电压为参考，这时式（4.62）变为

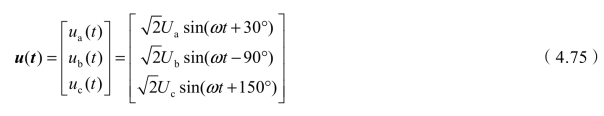
由此不难写出以A相电压为参考牵引侧最佳补偿电流表达式，此处不再赘述。

4）单台阻抗匹配平衡变压器接线

阻抗匹配平衡变压器接线次边为两相系统，与图3.8（a）所示的YN，d11接线连接方式相对应，α 相对应ab端口、β 相对应bc端口，所以，则

基准电压，代入式（4.67）可得，两相系统最佳补偿电流为

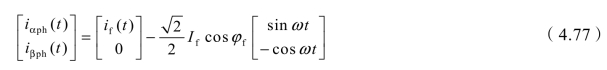
对应图3.8（b），α 相对应aF端口、β 相对应bc端口，所以，其余与图3.8（a）的情况完全相同。

阻抗匹配次边两相与原边A相电压有15° 和－75° 相角差，所以，如果以变压器原边A相电压为参考，那么式（4.77）变为

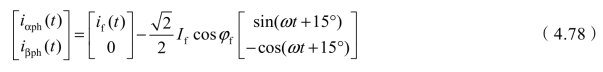
5）Scott接线

接线原理如图3.10所示，，由图可得

基准电压，代入式（4.67）可得，两相系统最佳补偿电流为

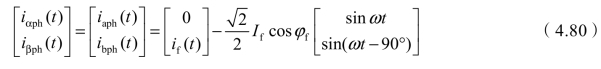
6）三相变四相变压器接线

接线原理如图3.9所示，根据三相变四相变压器的特点，可得

将上式和式（4.49）、式（4.50）代入式（4.59），可得