系统谐波对高速铁路供电的影响

非牵引负荷造成的电压波形畸变使系统电压中含有谐波成分，把这种谐波统称为系统谐波。为了便于观察系统谐波的影响，假定系统和负载完全对称，并将负载分为纯阻性负载和感性（容性）负载两种情况进行分析。由于三相完全对称，因此可以简化为单相系统进行分析，如图4.5所示。

假设系统电压含有谐波，即系统电压可表示为

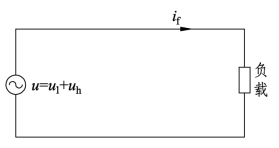
图4.5　单相电路模型

式中，u1（t）、uh（t）分别为系统基波电压分量和谐波电压分量。

1．当负载为纯阻性负载时

令负载的电阻为R，u1（t）、uh（t）分别作用于负载产生的功率损失为P1、Ph，则负载电流可表示为

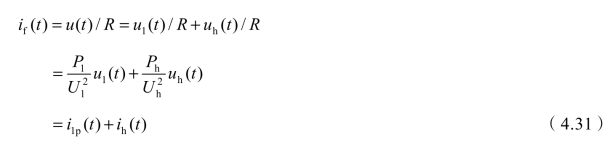
式中，i1p（t）为与u1（t）对应的基波电流，是u1（t）作用于负载产生的电流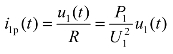，；ih（t）是由于uh（t）作用于负载而产生的谐波电流，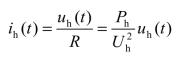

1）谐波对波形畸变最小模型的影响

根据波形畸变最小模型式（4.24），得

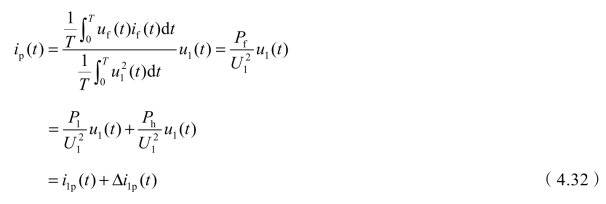
式中，，kh=Ph/P1为谐波功率相对系数。

由式（4.32）可见，对于波形畸变最小模型，系统提供的电流只有基波电流分量，它由两部分组成：第一部分与负载所消耗的基波有功功率成正比，且正好等于电源作用于负载所产生的基波有功电流；第二部分大小正比于系统谐波电压作用于负载所产生的谐波有功功率，由以下分析可知，它是从系统流向补偿装置。所以，系统除了向负载提供基波有功电流外，还额外向补偿装置提供了一基波电流Δi1p（t）。

根据注意式（4.31）和式（4.32）可求得补偿电流，为

式（4.33）说明，波形畸变最小模型的补偿电流也由两部分组成：第一部分为谐波电流，其大小正好等于系统作用于负载所产生的谐波电流，为了保证系统输出电流的波形质量，根据波形畸变最小模型要求，谐波电流必须由补偿装置提供；第二部分为基波有功电流，其大小正好等于补偿后的系统输出电流第二部分，前面有一个负号，说明是由系统流入补偿装置。各电流大小如图4.6（a）所示。

图4.6（b）进一步说明系统输出电流、负载电流和补偿装置提供的电流三者之间的关系。从图中可以清楚地看出，系统输出电流一部分直接流向了负载，其大小为i1p（t）正好等于负载的基波有功电流，另一部分流向了补偿装置，其大小为Δi1p（t）；补偿装置向负载提供谐波电流，其大小为ih（t）正好相当于谐波电压作用于负载产生的谐波电流。

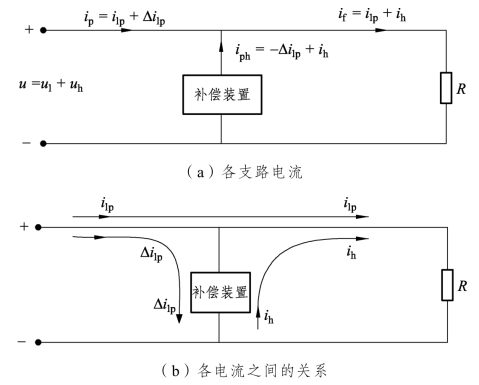
图4.6　系统谐波对波形畸变最小模型的影响

图4.6中有两种现象需要加以说明：一是虽然系统电压有谐波，但系统并不输出谐波电流；二是为什么系统还额外向补偿装置提供了基波有功电流Δi1p（t）。

根据波形畸变模型的要求，谐波电流必须由补偿装置提供，而补偿装置提供的谐波电流流过负载产生谐波电压ihR，正好等于系统的谐波电压uh，从而抑制了系统向负载输出谐波电流，保证了系统输出电流不含谐波。同时，由于谐波电流流过负载产生了功率损耗（其功率大小正好等于Ph），但是补偿装置不可能单向输出有功功率，否则变流器直流侧电容电压将降为零，从而无法正常工作，所以在四象限变流器直流侧电容电压自动调节器的作用下，系统向补偿装置额外提供了基波功率，其大小正好等于负载所消耗的谐波有功功率，从而确保了补偿装置输入输出的功率平衡。这就是为什么系统输出电流有一部分流入补偿装置的原因，相当于一部分基波有功功率Ph由系统经补偿装置转换为谐波功率流入了负载。

结论：对于纯阻性负载，在能量平衡和波形畸变最小模型的双重制约下，一部分基波电流i1p（t）直接由系统流向了负载，而另一部分基波电流Δi1p（t）则由系统流向补偿装置，再由补偿装置转化成谐波电流ih（t）流向负载，流入流出补偿装置的有功功率相等。结果是系统只输出基波电流，而输出的功率等于系统电压作用于负载所产生的基波与谐波有功功率的总和。

2）谐波对最佳负载模型的影响

根据最佳负载模型式（4.8），并注意if（t）=u（t）/R，可得

式（4.34）说明，最佳负载模型下系统提供的电流既有基波电流分量也有谐波电流分量，且其波形与系统电压波形完全相同。补偿电流为

式（4.35）说明补偿装置不提供任何电流。其电流关系如图4.7所示，可见这时补偿装置没有任何作用。为什么会出现这种现象呢？这是因为最佳负载模型的补偿目标是将负载变为对称纯电阻负载，而示例中的负载已经是三相对称的纯阻性的最佳负载了，所以没有必要再实施补偿了。至于负载中的谐波电流是由系统谐波造成的，并非由负载自身造成的，所以不应该补偿这部分谐波。

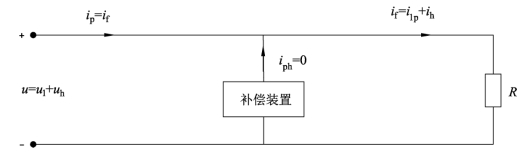
图4.7　系统谐波对最佳负载模型的影响

2．感性（容性）负载

当负载为感性（容性）的线性负载时，根据功率守恒原理，总可以把负载视为由只消耗有功功率的纯有功网络和只交换无功功率的纯无功网络两部分组成。纯有功部分可以等效为一个电阻，而纯无功部分可以视为由纯电感、电容构成的复杂网络。为了简化，下面以图4.8所示单相等效电路一般形式为基础进行分析，分析结果同样适用于其他情况。

由于系统电压含有谐波，当基波电压和谐波电压分别作用于电阻和电感（电容）时，将产生基波电流和谐波电流；同时，由于负载有有功功率损耗和无功功率损耗，所以负载中的电流又可分为有功电流和无功电流。因此，负载电流的瞬时值可表达为(www.xing528.com)

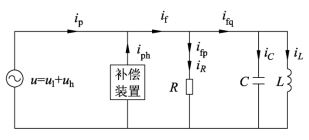
图4.8　感性负载单相等效电路

式中　ifp（t）、ifq（t）——广义有功电流和广义无功电流，对应于含有基波和谐波的电源电压分别作用于负载的电阻部分和电感（电容）部分产生的电流。

i1（t）、ih（t）——负载的基波有功电流和谐波电流，对应于电源的基波电压和谐波电压分别作用于负载产生的电流。

i1p（t）、i1q（t）——基波电压作用于负载产生的基波有功电流和基波无功电流。

ih（t）——由两部分组成：谐波电压作用于纯阻性负载产生的有功电流分量ihp（t）和谐波电压作用于纯感性（纯容性）负载产生的无功电流ifq（t）。

1）谐波对波形畸变最小模型的影响

根据波形畸变最小模型式（4.24），可得

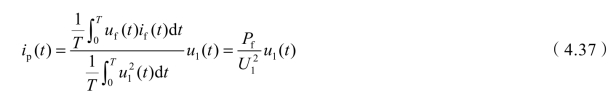
根据图4.8容易求得基波电压作用于纯阻性负载所产生的基波电流：

所以，式（4.37）可进一步写为

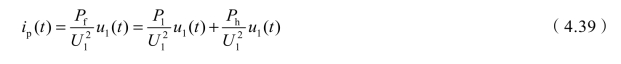
式（4.39）说明，在波形畸变最小模型下，即便是有感性（容性）负载，系统输出的电流也只有基波有功分量，且系统输出电流与电源的基波电压成比例，可以将其分为两部分：一部分为i1p（t），其幅值与基波有功功率成正比；另一部分为Δi1p（t），其幅值与谐波有功功率成正比。

补偿电流为

式（4.40）说明波形畸变最小模型下补偿装置输出电流由三部分组成：第一部分为基波无功电流，其大小等于系统的基波电压作用于负载所产生的基波无功电流，根据波形畸变最小模型要求，负载的无功电流必须由补偿装置提供；第二部分为谐波电流，其大小等于负载所需的谐波电流，根据波形畸变最小模型要求，负载中的谐波电流，也必须由补偿装置提供；第三部分为基波有功电流分量，其大小与谐波流过负载所消耗的有功功率成正比，前面有一负号，表示是由系统流入补偿装置。各电流大小及流向如图4.9（a）所示。

图4.9（b）进一步表明了各电流之间的关系。从图中可以清楚地看出：对于感性负载，在系统谐波作用下，补偿装置向负载提供了基波无功电流和谐波电流，而系统向负载提供基波有功电流，并额外向补偿装置提供了基波有功功率；系统向补偿装置输入的功率等于负载消耗的谐波有功功率。

图4.9　系统谐波对波形畸变模型的影响

2）谐波对最佳负载模型的影响

由于系统作用于纯电感（纯电容）的无功网络不产生有功功率损耗，所以电源电压与无功电流乘积的一个周期积分应为零，即。所以将（4.36）代入最佳负载模型式（4.8）可得

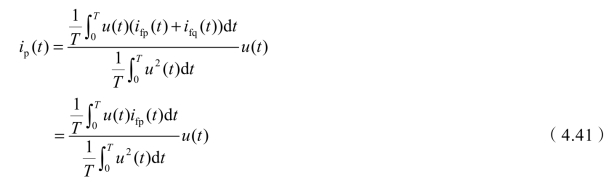
由图4.8知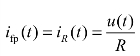，，将其代入（4.41）可得

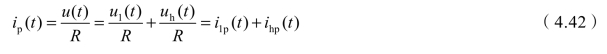
式（4.42）说明系统提供的电流与系统电压波形相同，且等于系统电压作用于只消耗有功功率的电阻（纯有功网络）中的电流，与只交换无功功率的无功网络部分无关。系统提供的电流由基波和谐波两部分组成：一部分相当于系统基波电压作用电阻产生的电流，称其为基波有功电流；另一部分相当于系统谐波电压作用于电阻产生的电流，称其为谐波有功电流。可见，系统输出的电流中有谐波成分，而这部分谐波并没有要求补偿，这是由最佳负载模型的特性决定的。

补偿装置提供的电流为

补偿电流等于流过纯无功网络，即电感（电容）中的电流，也就是说补偿装置只提供无功电流，相当于补偿前电源作用于纯无功网络产生的电流，包括基波无功电流和谐波无功电流。

各电流关系如图4.10所示。图4.10（a）为补偿模型电路，其中的电源电流等于电阻中的电流，而补偿装置提供的电流等于负载中的无功电流。图4.10（b）为补偿后的等效电路，可见，在最佳负载模型约束下，补偿后的负载对电源而言仅相当于一个只消耗有功功率的纯电阻负载。

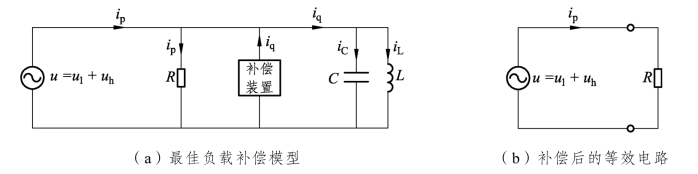
图4.10　谐波对最佳负载模型的影响

由于最佳负载模型补偿目标是将负载变为纯电阻的最佳负载，因此补偿后电源输出的电流正比于电源电压，当电源电压中有谐波时系统输出电流中也必然有谐波；而波形畸变最小模型的补偿目标是电源输出电流没有畸变、不含谐波。因此，即使系统电压含有谐波，而系统输出的电流中也不含谐波，全部谐波和无功电流都有补偿装置提供。

结论：对于波形畸变最小模型，系统谐波将导致一额外的有功功率穿越补偿装置，从而使补偿装置的负担加重；系统谐波含量越大，穿越功率也越大，补偿装置的负担也越重。这如同无源补偿中的谐波“倒灌现象”——由于谐波的补偿而使补偿点的谐波阻抗减小或接近于零，从而引起各处的谐波流向补偿点。谐波“倒灌现象”会使补偿装置负担加重，严重时还会导致补偿装置发热而损坏。最佳负载模型下的补偿电流仅与负载本身有关，负载所消耗的有功功率由电源直接提供，负载所消耗的无功功率由补偿装置提供，不存在波形畸变最小模型中的功率穿越现象和谐波“倒灌现象”。