高速铁路同相供电系统负载模型

同相牵引供电系统情况要复杂得多，变压器次边有三相（YN，d11接线）、两相（Scott接线）、四相（三相变四相接线）和单相等多种情况。但对于同相供电平衡补偿而言，总可以把它等效为三相或两相系统来处理。下面以YN，d11接线和Scott接线为例进行分析，其结论同样适用于其他接线形式。

与单相系统最佳负载模型相似，同相牵引供电系统最佳负载模型是指通过补偿使不对称的单相负载（包括补偿装置）对电源而言仅相当于一对称纯阻性负载，而对称纯阻性负载所消耗的总功率等于单相的牵引负荷所消耗的总有功功率。最佳负载模型下电源输出且仅输出牵引负荷所消耗的总有功功率。

YN，d11接线系统，其同相供电平衡补偿模型如图4.2所示所示。对电源而言，图4.2（a）中虚框部分等效于图4.2（b）所示的虚框部分，表示补偿后单相的牵引负荷变成了三相对称的纯阻性负载。

图4.2　YN，d11接线同相供电平衡补偿模型

Scott接线的两相系统，平衡补偿最佳负载模型如图4.3所示。对电源而言，图4.3（a）虚框部分等效于图4.3（b）所示的虚框部分，表示补偿后单相的牵引负荷变成了两相对称的纯阻性负载。

图4.3　Scott接线同相供电平衡补偿等效模型

对于三相四相接线系统，尽管牵引变压器次边为四相，但其应用于同相供电系统时，除了一次系统有中性接线点外，原理上与Scott接线系统相同，因此二者平衡补偿的等效模型也完全一样。

假定变压器为理想变压器，根据能量损失最小模型可得[69，70]：

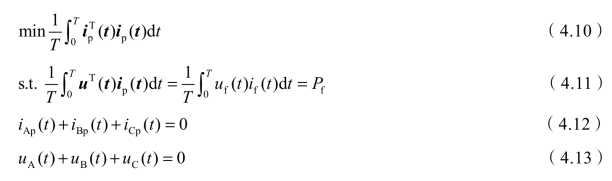
式中，ip（t）、i（t）、u（t）分别为同一侧各相广义瞬时有功电流矩阵、补偿前各相瞬时电流矩阵和各相瞬时电压矩阵。通常我们关注系统一次侧或牵引变压器二次侧（牵引侧）电气量，所以，ip（t）、i（t）、u（t）也对应为系统一次侧或牵引变压器二次侧（牵引侧）电气量。

若为系统一次侧时，ip（t）=[iAp（t）iBp（t）iCp（t）]T，其中，iAp（t）、iBp（t）、iCp（t）分别为最佳负载模型下系统一次侧三相瞬时电流，也称为系统一次侧广义瞬时有功电流；i（t）=[iA（t）iB（t）iC（t）]T，其中，iA（t）、iB（t）、iC（t）分别为补偿前系统一次侧三相瞬时电流；u（t）=[uA（t）uB（t）uC（t）]T。

若为系统二次侧时，对于YN，d11接线，则ip（t）=[iap（t）ibp（t）icp（t）]T，其中，iap（t）、ibp（t）、icp（t）分别为最佳负载模型下牵引变压器二次侧三相瞬时电流；i（t）=[ia（t）ib（t）ic（t）]T，其中，ia（t）、ib（t）、ic（t）分别为补偿前牵引变压器二次侧三相瞬时电流；u（t）=[ua（t）ub（t）uc（t）]T。对于Scott接线，ip（t）=[iαp（t）iβp（t）]T，其中，iαp（t）、iβp（t）分别为最佳负载模型下牵引变压器二次侧两相瞬时电流；i（t）=[iα（t）iβ（t）]T，其中，iαp（t）、iβp（t）分别为补偿前牵引变压器二次侧两相瞬时电流；u（t）=[uα（t）uβ（t）]T。

目标函数式（4.10）代表能量传输损失最小；约束条件式（4.11）说明电源仍应提供且只提供负载所消耗的全部有功功率，无功功率应有补偿装置提供。式（4.12）和式（4.13）为牵引供电系统固有的条件。

对式（4.10）和式（4.11）求解，可令

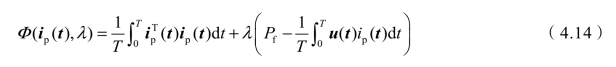(www.xing528.com)

Φ（ip（t），λ）的增量可表述为

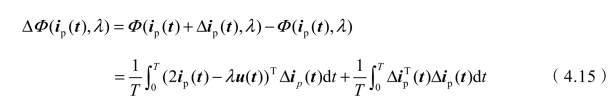
显然对于任意Δip（t）≠0都有。所以，式（4.10）的最小值必然存在。根据泛函极值及变分原理，式（4.10）最小值条件为

将式（4.17）代入式（4.11）可得

将式（4.18）代入式（4.17）可得

式中，G为广义有功电流与电压的比例常数，当三相电压对称时，

以上是根据功率传输损失最小原理求得的广义有功电流ip（t），也可以根据同相供电最佳负载模型的定义直接确定ip（t）。根据最佳负载模型的定义，补偿后ip（t）与u（t）成比例，可令ip（t）=Gu（t），并代入式（4.11）求得常数G，最后可得到式（4.19）。

定义系统的广义瞬时无功电流矩阵为

最佳负载模型下为了达到补偿目标，平衡补偿电流iph（t）应等于广义瞬时无功电流，即

从式（4.19）可以看出，广义瞬时有功电流的大小与负载的有功功率成正比，而与负载接入的端口无关。以三相系统为例，如果三相电压对称，则补偿后电源提供的三相有功电流对称；如果三相电压不对称，则补偿后电源提供的三相有功电流也不对称；如果电源电压中含有谐波，则补偿后电源提供的电流中也必然含有谐波。