单相系统最佳负载模型

单相系统等效电路如图4.1（a）所示，其最佳负载模型如图4.1（b）所示。

通常电源向负载提供的能量由两部分组成：一部分被负载所消耗；另一部分负载本身并不消耗而是在负载与电源之间往复交换。定义单位时间内负载所消耗的能量为有功功率，单位时间内往复交换的能量为无功功率。往复交换的能量只会增加电源的负担和传输损耗，这部分能量越大，则传输损耗越大。根据能量损失最小原理[65，66]，可得数学表达式为

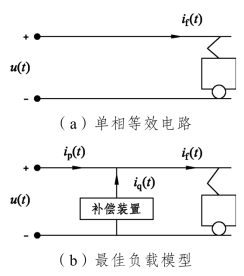
图4.1　牵引侧最佳负载模型

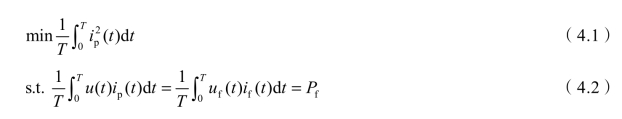
式中　if（t）——牵引负荷电流；

uf（t）——牵引负荷端口电压，就是牵引网电压，在此uf（t）=u（t）；

ip（t）——广义瞬时有功电流。

以上两式是关于平衡补偿的最优化问题。

由于电能传输损失与电流的平方成正比，所以目标函数式（4.1）代表了能量传输损失最小；约束条件式（4.2）表明负载所消耗的有功功率应该由电源全部承担，补偿装置只提供无功功率。对式（4.1）、式（4.2）最优化数学模型求解[67，68]，可令

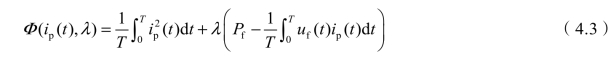
其中，Φ（ip（t），λ）一般称其为拉格朗日函数；λ 为拉格朗日乘数。Φ（ip（t），λ）的增量可表述为(www.xing528.com)

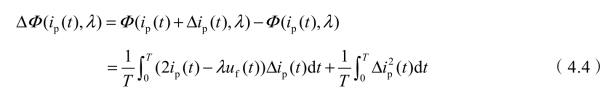
等式右边第一项为增量的线性部分，称为拉格朗日函数的变分；等式右边第二项为增量的高级无穷小项，显然对于任意Δip（t）≠ 0都有。所以，式（4.1）的最小值必然存在，根据泛函极值及变分原理，式（4.1）最小值条件为

将式（4.6）代入式（4.2）可得

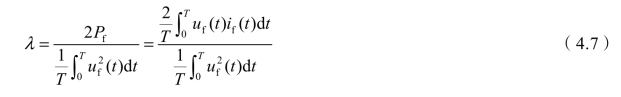
将式（4.7）代入式（4.6）得

式中　G——比例常数，G=Pf/U2，Pf、U分别为负荷的有功功率和牵引网电压有效值，即。

其实，按照最佳负载模型定义很容易求出ip（t）。根据最佳负载模型的定义，通过补偿使负载对电源而言仅相当于一个纯阻性负载，所以ip（t）必然与uf（t）成正比。假设ip（t）=Guf（t），将其代入式（4.2）并注意u（t）=uf（t）、，可得G=Pf/U2，再由假设可得式（4.8）。这也说明最佳负载模型符合能量损失最小原则。

定义广义瞬时无功电流为：

如果负载为最佳负载，即if（t）=Guf（t），则iq（t）=0，这时负载只消耗有功功率，不需要实施无功补偿。实际中负载通常不是纯阻性的，会从电网吸收一定的无功功率。为了减小功率损失，需要增设无功补偿装置。从图4.1（b）可以看出，当补偿装置提供的电流为广义无功电流时，电源提供的电流恰好为广义有功电流，补偿后的负载相当于一个纯阻性负载，此时传输能量损失达到了最小。