高速铁路同相供电补偿原理

在20世纪80年代，西南交通大学李群湛教授倡导采用同相供电，并针对中国电气化铁道牵引供电系统实际情况，为了消除或减小负序电流的影响，提出了无源对称补偿技术。无源对称补偿技术是通过在牵引侧端口上并联无功补偿（PRC）装置或并联电容补偿（PCC）装置来消除或削弱系统不平衡[42-46]。以YN，d11接线变电所为例，在牵引侧三个端口上并联补偿装置，如图2.9所示，图中原次边各相绕组平行对应。设牵引侧各端口编号依次为1、2、3、4，其中1号端口接负荷，2、3、4号端口接补偿装置。

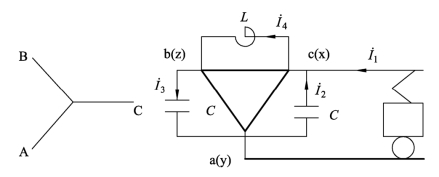
图2.9　YN，d11接线同相供电对称补偿系统

1．负序的补偿

以为参考，本例1号端口与2号端口重合，因此各端口接线角分别为ψ1=ψ2=0°，ψ3=120°，ψ4=-1 20°；各端口的接线系数分别为K1、K2、K3、K4，由于各端口电压相等，所以K1=K2=K3=K4=1；如果负荷的功率因数角滞后40°，根据式（1.108）可得各端口产生的负序电流分别为

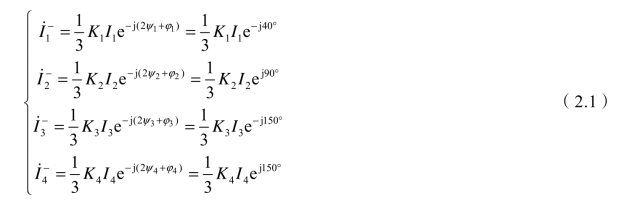
若要完全消除不平衡，则总负序电流应为零，所以

式中、φ1——牵引负荷的电流及其功率因数角；

、φm（m=2，3，4）——补偿端口m的补偿装置电流及功率因数角；

ψm（m=2，3，4）——端口m的接线角。

式（2.2）中左侧为各补偿端口产生的负序电流总和，右侧为牵引负荷端口产生的负序电流，其中负号表示负序向量反向，说明当各补偿端口所产生的总负序电流与牵引负荷端口产生的负序电流大小相等、方向相反时，系统中的总负序电流为零。

复数相等，则两边虚实部应该分别相等，由式（2.2）可得

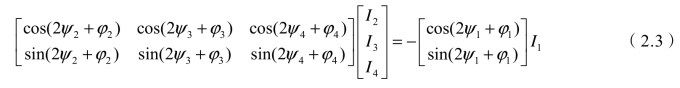
显而易见，式（2.3）最多有两个解，说明在两个端口上安装补偿装置能够完全补偿负序，两个端口之外任意一个端口上安装补偿装置对于仅补偿负序来说都是多余的。若仅在2、4端口上加补偿装置，以为参考，负荷的功率因数角为40°，这时各端口负序向量图如图2.10所示。可见两个补偿端口产生的负序电流向量的合成向量与负荷产生的负序电流向量，正好反向。

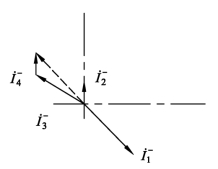
图2.10　负序向量图

2．负序和无功同时补偿

定义负序补偿度KN∈[0，1]为对称补偿装置产生的总负序容量与牵引负荷产生的总负序容量之比值。对式（2.2）两端取共轭并乘以端口电压有效值，考虑负序补偿度可得

式中　S1——牵引负荷容量；

Sm（m=2，3，4）——补偿端口m的补偿装置容量，容性为正，感性为负。

定义无功补偿度Kc∈[0，1]为对称补偿装置总（容性）无功功率与牵引负荷（感性）无功功率之比值；牵引负荷总无功功率为S1sin φ1，根据负荷无功与补偿无功之间的关系，有

由式（2.4）和式（2.5）可得以下方程组：

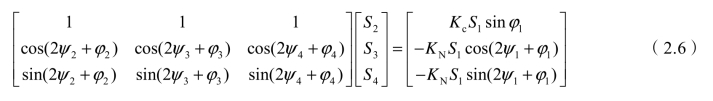
当牵引变压器和牵引负荷一定时，对于任意给定的无功补偿度Kc和负序补偿度KN，根据式（2.6）总能求出各端口补偿装置容量Sm（m=2，3，4）。说明从理论上讲，任何一种牵引变压器，应用对称补偿技术，均能完全补偿无功和负序，使系统三相电流对称，即可构成三相-单相对称变换系统，实现同相供电。

仍以图2.9情况为例，将各端口接线角代入式（2.6）解得

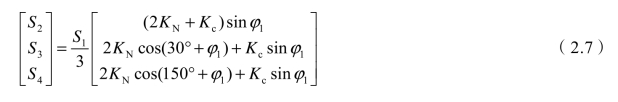(www.xing528.com)

若牵引负荷的容量为10 MVA，功率因数为0.8（滞后），要求补偿后功率因数达到0.9（当Kc=0.354时功率因数刚好为0.9），负序完全补偿（KN=1），则由上式求得S2=4.71 MVA（容性），S3=3.33 MVA （容性），S4=5.91 MVA （感性），则S2+S3+S4=14 MVA，所以S2+S3+S4≥ S1。

由以上分析可知：

（1）基于常规变压器实施对称补偿时，由于各端口的接线角固定不等，各端口补偿装置所产生的负序电流都不能与牵引负荷产生的负序电流反向共线，从而使得补偿装置的总安装容量（完全补偿时）大于牵引负荷容量，补偿设备利用率不高，造成容量浪费。

（2）牵引负荷是动态变化的，但电容和电感难以动态调整，所以无法动态补偿无功和负序。

（3）从补偿无功功率角度看，感性与容性补偿功率是相互削弱的，为了减小不必要的容量浪费，补偿无功时希望各端口补偿装置都是容性；但补偿负序时必须一个容性、一个感性（见下节），二者永远是矛盾的。

3．最小设备容量条件

综合补偿时，为了使补偿装置设备容量达到最小，则各端口补偿支路所产生的负序电流都应与牵引负荷所产生的负序电流反向共线，考虑容性和感性容量一个为正、一个为负，则，式（2.4）和式（2.5）变为[42]

式（2.8）两个方程只能有两个解，说明：为了达到最理想的补偿状态，必需且只须在某两个端口设置补偿装置；如果这两个端口的补偿装置性质相同（同为容性或同为感性），则方程无解，故两个端口补偿装置必然一个为容性、一个为感性。设容性补偿端口的容量为SC，感性补偿端口的容量为SL，代入式（2.8）变为

由于各补偿端口所产生的负序电流都应与负荷引起的负序电流反向共线，所以等式（2.4）两边的幅角应相等，即2ψm+φm=±180°+2ψ1+φ1，因此

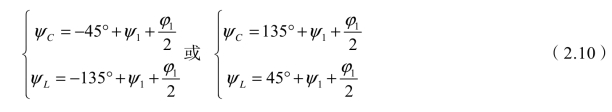
式中，ψC为容性端口的接线角；ψL为感性端口的接线角。

式（2.10）表明实现同相供电最佳对称补偿的条件是两个补偿端口的电压矢量互相垂直。目前常用的YN，d11接线变压器和V，v接线变压器不能提供电压相互垂直的两个端口，所以不能实现最佳补偿；Scott接线变压器和阻抗匹配平衡变压器，尽管能够提供电压相互垂直的两个端口，但无论电容、电感补偿端口和负载端口如何选择，ψC、ψL、ψ1都无法满足式（2.10），故不能实现最佳补偿。因此，采用特殊接线方式变压器是实现最佳对称补偿的唯一途径。实现同相供电对称补偿的特殊接线方式主要有不等边Scott接线、不等边YN，vd接线、不等边V，v接线和YN，2d接线等[28]。下面以不等边Scott接线为例说明其对称补偿的基本原理。

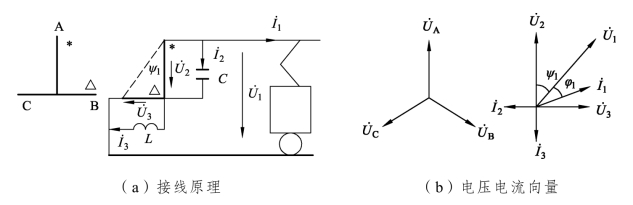
图2.11　不等边Scott接线对称补偿系统

不等边Scott接线与普通的三相-两相平衡Scott接线相似，输出电压相位垂直只是大小不等。不等边Scott接线同相供电对称补偿系统接线原理和电压电流相量关系，如图2.11所示。其中端口1接牵引负荷，端口2接并联电容，端口3接并联电抗。由图2.11（a）可知ψC=0、ψL=-9 0°，因此，最佳补偿时牵引端口的接线角ψ1可由式（2.10）求得

假设牵引负荷功率因数 φ1=30°，则ψ1=30°。根据式（1.108）求得产生的负序电流为

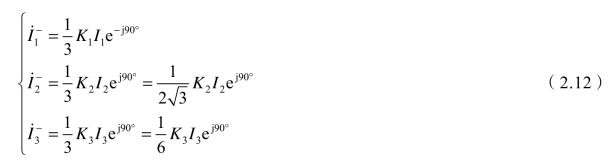
各端口产生的负序电流向量如图2.12所示，补偿电流产生的负序电流与牵引负荷产生的负序电流反向共线，从而可以使补偿设备容量得到充分利用。由式（2.9）可求出补偿电容器容量和补偿电抗器容量为

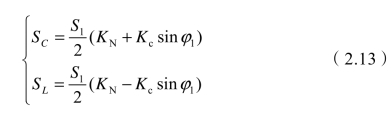
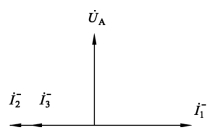
图2.12　负序电流向量

由式（2.11）、式（2.12）和式（2.13）可得如下结论：

（1）因为SC+SL=KNS1，所以补偿装置在任何情况下的总投入容量都不会超过牵引负荷容量。

（2）由于牵引负荷功率因数的波动性，必须按照式（2.11）实时调整接线角ψ1，否则无法达到最佳补偿的目的。因为如果接线角ψ1不满足式（2.11），则补偿装置产生的负序电流与牵引负荷产生的负序电流就不可能反向共线，从而也就不可能完全实现对称补偿和补偿设备容量的充分利用。为了能够调整接线角ψ1，则次边应有一个绕组匝数可调，实现难度较大，为此实际中固定绕组匝数而按平均功率因数确定接线角ψ1。这样对于变化的牵引负荷也就不可能达到最佳补偿的要求。

（3）为了达到最佳补偿要求，必须根据牵引负荷的容量和功率因数的变化按照式（2.13）实时调整补偿装置的容量。在实际中电抗器可以做到连续可调，而电容器只能分级可调，所以无源补偿装置无法实现对负序和无功的动态最佳补偿。