高速铁路系统不平衡对策

由于交流电气化铁道牵引负荷——电力机车为变化频繁的单相负荷，它将在电力系统中产生较大的负序电流，造成三相严重不平衡。不平衡程度与牵引负荷的大小及其分布状况、变电所主变压器接线形式有关。以下针对当前主要采用的接线形式，包括单相接线、V，v接线、YN，d11接线、阻抗匹配平衡接线和Scott接线，所造成的三相系统不平衡做简要分析。

1．正序与负序电流

当前电气化铁道常用的接线形式，其变压器一次侧都是三相系统，其二次侧分别有两相、三相、四相系统等多种形式。为不失一般性，假设要讨论的模型一次侧为三相、二次侧为n相系统，且一、二次侧都是星形接线，如果不是星形接线（如YN，d11接线二次侧为三角接线），则可以按照1.1.3节所示的等效原理将其等效为星形接线。

假设有k个端口有牵引负荷，第m个端口的电压和电流分别为

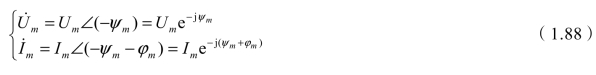
式中，分别为m端口负荷的电压和电流向量；ψm为m端口的电压滞后基准电压（如果是求系统一次侧的正、负电流，则基准侧为系统一次侧，基准电压一般选取为；如果基准侧为变压器二次侧，则基准电压一般选取为a相星形等效电压）的相位角，称为负载接线角，并定义滞后时为正； φm为m端口负载的功率因数角。

1）三相系统

（1）三相系统的正序电流。

设系统电压完全对称，这时电压只有正序分量，其余各序分量都为零，即，根据功率守恒原理，得

式中——求和符号，在此表示对各端口牵引负荷造成的影响求总和；

A——三相对称变换矩阵，，为A的共轭，E为单位矩阵；

——原边三相电压和电流向量矩阵；——原边三相电压和电流的零序、正序和负序分量矩阵，下标“0”代表零序，“1”代表正序，“2”代表负序。

记，将式（1.88）代入式（1.91），两边取共轭并整理可得

式中，Km为第m端口的负载接线系数，等于负载端口电压有效值与基准电压有效值之比值。由于三相电压对称，基准电压等于正序电压，又由于通常情况下取A相电压为基准电压，所以，Km=Um/U1=Um/UA。

（2）三相系统的负序电流。

当系统三相电压对称时，根据功率守恒式（1.38），有

注意到，故

所以

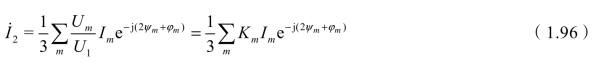
2）牵引变压器二次侧，n相系统正序与负序电流

为不失一般性，假设系统有n相，根据多相对称分量法，各相向量与各序分量之间关系为

式中，分别代表n相电压或电流向量矩阵；分别代表n相（等效星形）电压或电流各序分量矩阵；A为对称变换矩阵，且对于n相系统，对称变换矩阵A为

式中，a=1∠（2 π/ n）为旋转因子，且1+a +a2+…+an-1=0；式（1.98）对于所有n ＞2的n相系统都适用，尤其当n=3时，则a=1∠ 1 20°=1∠（2 π/3），这时A就是我们熟悉的三相系统对称变换矩阵。

n=2时的两相系统比较特殊，需要另外定义。本节讨论的两相系统是指相位相差90°的系统，可以看作四相系统的特例，即a=1∠ 9 0°=1∠（π/2），两相系统的对称变换矩阵定义为

经以上定义，两相、三相和四相系统的各相向量与各序分量之间关系可以统一用式（1.97）表达，且任意n相系统对称变换矩阵都满足。n相系统对应n个序分量，但是对于牵引供电系统来讲，只有正序和负序分量有意义。为不引起混淆，定义顺相序的分量为正序，统一用下标“1”表示；逆相序的分量为负序，统一用下标“2”表示。

（1）n相系统的正序电流。

设n相等效星形电压完全对称，这时电压只有正序分量，其余各序分量都为零，根据功率守恒得

式中，、分别代表n相系统的电压、电流向量矩阵；、与三相系统不同，在此分别代表n相电压和电流的各序分量矩阵，由式（1.101）得

（2）n相系统的负序电流。

仍假设系统的n相电压完全对称，这时电压只有正序分量，其余各序分量都为零，，根据功率守恒伴随式（1.38），则

记，将式（1.88）代入式（1.106），可得

从以上分析可以看出，任意的n相系统，由牵引负荷引起的牵引变压器各侧的正、负序电流表达式完全相同。为示区别，以下将正、负序电流统一用、表示，则正、负序电流统一表达式为

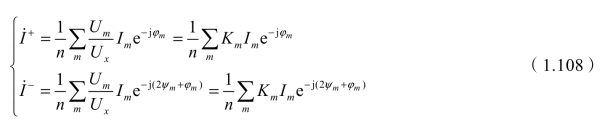
式中，Km为第m端口的负载接线系数，等于负载端口电压与基准电压之比值，Km=Um/Ux，Ux为基准电压，一般以待求侧的等效星形A相（或a相或α 相）电压为基准电压，由于系统电压对称，所以基准电压等于正序电压，即Ux=U1。式（1.108）还可写成如下形式：

式中，Sm=UmIm为m端口负载容量（负载的视在功率）。

式（1.109）可见，正、负电流大小与基准电压有关，这是容易理解的，因为不同电压等级下，如变压器原边和次边的电流大小自然是不同的。考虑系统的功率守恒，定义各侧统一的基准容量为Sj，待求侧的基准电流为Ix，且Ix=Sj/（nUx）。将基准电流代入式（1.109），并假定只有一个端口（m端口）有负荷，得

式中——m端口负荷容量标么值，；

——基准侧正、负序电流向量标么值。

从式（1.110）可以看出，正、负序电流大小只与负荷容量有关，与负荷接入的端口无关。

结论：

（1）某端口负荷所引起的正、负序电流的标么值恒等于该端口负荷容量的标么值；正、负序电流的大小与该端口负荷的容量（视在功率）成正比，而与负荷接入的端口无关。(www.xing528.com)

（2）某端口负荷所引起的正序电流的相位角等于负荷的功率因数角，与负荷接线角无关；某端口负荷所引起的负序电流的相位角等于负荷的功率因数角与两倍的负荷接线角之和。

2．不同接线方式时的正负序电流

由于以下讨论的是三相系统的正负序电流，因此式（1.108）中n=3 。

1）纯单相接线时三相系统的负序电流

纯单相接线次边仅有一个可供使用的端口，所以负载只能接入该唯一端口，如图1.22所示。图中变压器原边绕组接AB相间，所以负荷端口的接线角为ψ1=-3 0°。实际中变压器原边绕组可能接BC、CA相间，所以负荷端口的接线角有三种不同取值，如表1.5所示。

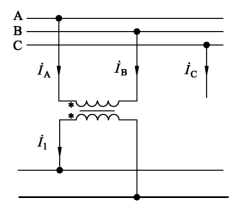
图1.22　单相接线

表1.5　单相接线时端口的接线角

定义电流不对称系数KI为负序电流与正序电流之比值，显然单相接线正序和负序电流大小相等，电流不对称系数KI=1，三相不对称程度十分严重。

由于牵引侧只有一个可供使用的端口，而补偿负序必须有另外一个不同接线角的端口。因此对于单相接线情况，要实现平衡补偿就必须额外增加补偿变压器，并能提供不同于负荷端口接线角的补偿用端口。

2）V，v接线时三相系统的正负序电流

这种接线牵引侧有两个端口，三相系统的正序和负序电流可认为是由两个端口的负荷电流、独立作用产生的三相系统正序和负序电流的叠加。对于图1.23接线，两个端口的接线角分别为ψ1=-3 0°、ψ2=90°，所以总正序电流和总负序电流，可由式（1.108）得

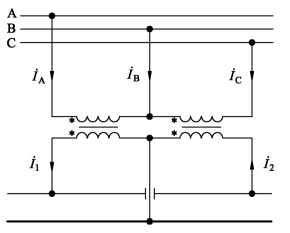
图1.23　V，v接线

一般情况K1=K2，根据式（1.111）可求得电流不对称系数。当I1=I2、φ1=φ2时，则电流不对称系数为0.5；当I1≠ I2时，电流不对称系数将大于0.5；当I1、I2其中一个为零时，则电流不对称系数为1。所以电流不对称系数变化范围为KI=0.5 ～1，系统不平衡程度仍很严重。

3）YN，d11接线时三相系统的正负序电流

如图1.24所示，这种接线同样有两个端口，端口的接线角分别为ψ1=0°、ψ2=-1 20°，根据式（1.108），则三相系统总正序电流和总负序电流分别为

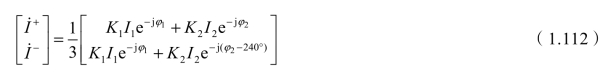
一般情况K1=K2=K 。若两端口负荷电流大小相等、相位相同，也即I1=I2、φ1=φ2时，则电流不对称系数KI=0.5；当一个端口有负荷，另一端口无负荷时，不对称系数最大KI=1。所以电流不对称系数的变化范围为KI=0.5 ～1。

由于端口相别可能是A、B和C相，所以端口的接线角有0°、120°、－120°三种取值，如表1.6所示。

表1.6　YN，d11接线时端口的接线角

4）阻抗匹配平衡接线时三相系统的正负序电流

如图1.25所示，这种接线同样有两个端口，两个端口的接线角分别为ψ1=-1 5°、ψ2=75°，并令K1=K2=K，代入式（1.108）可得

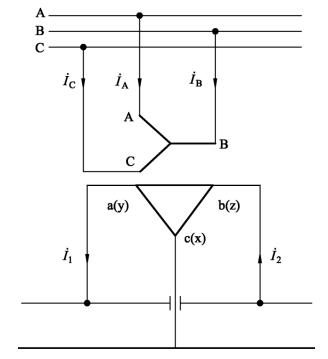
图1.24　YN，d11接线

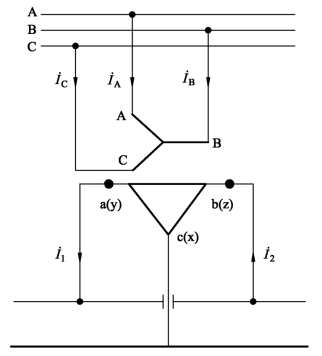
图1.25　阻抗匹配平衡接线

若两端口负荷电流大小相等、功率因数相同，也即I1=I2、φ1=φ2时，，阻抗匹配平衡变压器原边三相电流对称，电流不对称系数KI=0，这就是采用平衡变压器的优势所在。但是，根据对有关山区单线牵引变电所实测负荷统计，两供电臂同时有牵引负荷的概率很小，当一供电臂出现较大牵引负荷时，时常是另一个供电臂没有负荷。当仅有一个供电臂有负荷时，KI=1。所以变电所即使采用阻抗匹配平衡变压器接线，多数情况下系统仍是不平衡的。电流不对称系数的变化范围为KI=0 ～1。

5）Scott接线时三相系统的正负序电流

如图1.26所示，两个端口的接线角分别为ψ1=90°、ψ2=0°，代入式（1.108），并令K1=K2=K，可得

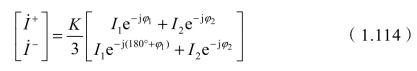
与阻抗匹配平衡变压器相同，当两个端口（M座和T座两供电臂）负荷电流相等、功率因数相同时，即I1=I2、φ1=φ2时，，电流不对称系数最小KI=0；当只有一个端口有负荷时，正负序电流大小相等，电流不对称系数最大KI=1。电流不对称系数的变化范围为KI=0 ～1。

图1.26　Scott接线

3．解决不平衡问题的一般对策

由于单相牵引负荷的随机性和剧烈波动性，无论采用哪一种接线方式，都将导致三相电力系统不对称而产生负序电流。负序电流对电力系统的危害和影响是十分严重的，这主要表现在：一是造成系统网络节点电压不对称，降低三相电动机出力；二是负序电流在电网中产生负序功率损失，降低了电网的运行效益；三是负序电流在发电机定子中产生和转子旋转方向相反的空间旋转磁场，它以二倍同步转速切割转子导体，在其中产生感应电势，致使转子附加发热，严重时导致转子绕组烧损。为了防止对电力系统和电力设备带来严重影响，各国对负序电流都有严格的限制标准。为了使系统不平衡程度限制在规定标准以内，当前主要采取以下几种措施[26-29]：

（1）采用三相-两相平衡牵引变压器，如阻抗匹配平衡变压器、Scott变压器、变形Wood-bridge变压器等[30-32]。这些变压器的优点是，当两个端口负荷完全相同时，变压器原边三相电流对称。即使两个端口负荷不相同，也会使不平衡度有所减弱。在日本广泛采用Scott变压器和变形Wood-bridge变压器，我国主要采用阻抗匹配平衡变压器和Scott变压器。

（2）采用高电压、大容量电源供电。因为高电压、大容量电源系统具有较强的承受不平衡负荷的能力。如日本采用154 kV、220 kV和275 kV三种电压等级，法国采用235 kV电压等级，意大利采用130 kV等级，西班牙采用132 kV、220 kV两种电压等级。

（3）采用不平衡补偿装置[33-35]，如日本采用单相负荷补偿装置（SFC）。

（4）采用换相连接，也就是各牵引变电所变压器原边轮换接入电力系统不同相，这样可以减小系统总负序电流。由式（1.108）可知，当两个端口的接线角相差90°、三个端口的接线角分别相差60° 或120° 时，端口负荷作用的结果，将使三相总负序电流减小。换相连接的原则：一是尽可能使各相负荷均匀，尽管各供电臂上的负荷是随机的，但只要按照相同的频率依次轮换接入不同的相别就可以大大减小不对称程度；二是在使各相负荷均衡的前提下，尽量使分相绝缘器承受较小的电压。按照这两条原则，单相接线和YN，d11接线换相连接的牵引供电系统示意图，如图1.27（a）、（b）所示[1]。

图1.27　换相连接牵引供电系统示意图

对于单相接线，由于换相连接后，牵引侧各端口电压相别依次为AB、AC、BC、BA、CA、CB、AB，所以端口的接线角依次为－30°、30°、90°、150°、－150°、－90°、－30°。假定各端口牵引负荷完全相同，即大小相等功率因数角相同，由式（1.108）可以验证，任意三个相邻端口相同牵引负荷时所产生的三相系统负序电流总和为零。设三个端口的接线系数为K，负荷电流有效值为I，功率因数角为φ，以AB、AC、BC三个端口为例，由式（1.108）得三个端口牵引负荷在系统中造成的总负序电流为

若从图1.27（a）左边依次标记端口序号为1、2、3、…，则各端口单独作用造成的三相系统负序电流为、…，向量图如图1.28（a）所示。从向量图容易看出，在各端口负荷相同时，换相连接后任意三个相邻端口牵引负荷所产生的负序电流大小相等、相位互差120°，所以在系统中产生的负序电流总和为零。当然任意六个相邻端口相同牵引负荷在系统中所产生的负序电流总和也为零。

对于YN，d11接线，换相连接后，牵引侧各端口电压相别依次为A、－B、－B、C、C、－A、－A、B、B、－C、－C、A，所以端口的接线角依次为0°、－60°、－60°、－120°、－120°、－180°、…。假定各端口牵引负荷完全相同，即大小相等、功率因数角相同，由式（1.108）可以验证，任意三个异相端口或任意六个相邻端口相同牵引负荷所产生的三相系统负序电流总和为零。设六个端口的接线系数用K表示，负荷电流有效值为I，功率因数角为φ，以A、－B、－B、C、C、－A六个端口为例，由式（1.108）得六个端口牵引负荷在系统中造成的总负序电流为

各端口负荷独立作用造成的三相系统负序电流向量图，如图1.28（b）所示。从向量图容易看出，在各端口负荷相同时，换相连接后任意六个相邻端口或三个异相端口，在相同牵引负荷条件下所产生的负序电流大小相等、相位互差120°，所以负序电流总和为零。

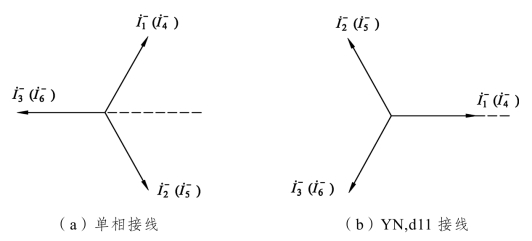
图1.28　换相连接后各端口负序电流向量图